题目内容
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),GM∥AB.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
•
=-2?若存在,求出直线l的方程,若不存在,说明理由.
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
=
=
=
.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
| OP |
| OQ |
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
可设C点的坐标为(x,y).
由重心坐标的公式,可得G(
x,
y)
外心M在AB的垂直平分线上,显然AB所在直线为y=0,外心就落在y轴上,横坐标为零;
设外心坐标M(0,b),由GM∥AB可知
y=b
那么就确定了外心坐标M(0,
y)
由外心定义,CM=AM=BM,AM已经等于Bm了,只需要令CM=AM或者CM=BM即可
不妨CM=AM,
∴x2+(y-
y)2=(-1-0)2+(
y)2
整理可得点C的轨迹方程为 x2+
=1(xy≠0)
(II)假设存在直线l满足条件,设直线l方程为y=kx+1,
由
消去x,得(3+k2)x2+2kx-2=0
∵直线l与曲线E并于P、Q两点,∴△=4k2+8(2+k2)>0
设P(x1,y1),Q(x2,y2),则
∵
•
=-2,
∴x1x2+y1y2=-2,即x1x2+(kx1+1)(kx2+1)=-2.
(1+k2)x1x2+k(x1+x2)+3=0,(1+k2)(-
)+k(-
)+3=0
解得k2=7,∴k=±
故存在直线l:y=±
+1,使得
•
=-2,
由重心坐标的公式,可得G(
| 1 |
| 3 |
| 1 |
| 3 |
外心M在AB的垂直平分线上,显然AB所在直线为y=0,外心就落在y轴上,横坐标为零;
设外心坐标M(0,b),由GM∥AB可知
| 1 |
| 3 |
那么就确定了外心坐标M(0,
| 1 |
| 3 |
由外心定义,CM=AM=BM,AM已经等于Bm了,只需要令CM=AM或者CM=BM即可
不妨CM=AM,
∴x2+(y-
| 1 |
| 3 |
| 1 |
| 3 |
整理可得点C的轨迹方程为 x2+
| y2 |
| 3 |
(II)假设存在直线l满足条件,设直线l方程为y=kx+1,
由
|
∵直线l与曲线E并于P、Q两点,∴△=4k2+8(2+k2)>0
设P(x1,y1),Q(x2,y2),则
|
∵
| OP |
| OQ |
∴x1x2+y1y2=-2,即x1x2+(kx1+1)(kx2+1)=-2.
(1+k2)x1x2+k(x1+x2)+3=0,(1+k2)(-
| 2 |
| 3+k2 |
| 2k |
| 3+k2 |
解得k2=7,∴k=±
| 7 |
故存在直线l:y=±
| 7 |
| OP |
| OQ |

练习册系列答案
相关题目
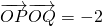 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.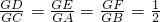 .
.