题目内容
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),且(1)求点C的轨迹E的方程;
(2)是否存在直线l,使l过点(0,1)并与曲线E交于P、Q两点,且满足![]() ·
·![]() =-2?若存在,求出直线l的方程;若不存在,说明理由.
=-2?若存在,求出直线l的方程;若不存在,说明理由.
解:(1)设C(x,y),其中xy≠0.由![]() =λ
=λ![]() (λ∈R且λ≠0),知MG∥AB.设G(a,b),则M(0,b),∴x=3a,y=3b①.
(λ∈R且λ≠0),知MG∥AB.设G(a,b),则M(0,b),∴x=3a,y=3b①.
∵M是不等边△ABC的外心,∴|MA|=|MC|,∴![]() =
=![]() ②,
②,
将①代入②化简整理得x2+![]() =1.所以点C的轨迹E的方程为x2+
=1.所以点C的轨迹E的方程为x2+![]() =1(xy≠0).
=1(xy≠0).
(2)假设存在直线l满足条件,设直线l方程为y=kx+1,
由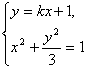 消去y得(3+k2)x2+2kx-2=0.
消去y得(3+k2)x2+2kx-2=0.
∵直线l与曲线E交于P、Q两点,∴Δ=4k2+8(3+k2)>0.
设P(x1,y1),Q(x2,y2),
则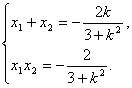
∵![]() ·
·![]() =-2,∴x1x2+y1y2=-2,
=-2,∴x1x2+y1y2=-2,
即x1x2+(kx1+1)(kx2+1)=-2,
(1+k2)x1x2+k(x1+x2)+3=0,(1+k2)(-![]() )+k(-
)+k(-![]() )+3=0,解得k2=7,k=±
)+3=0,解得k2=7,k=±![]() .
.
故存在直线l:y=±![]() +1,使得
+1,使得![]() ·
·![]() =-2.
=-2.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.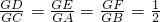 .
.