摘要:曲线y=-与曲线y+|ax|=0 (a∈R)的交点个数一定是( ). (A)2个 (B)4个 (C)0个 (D)与a的取值有关 提示:取特殊值法.
网址:http://m.1010jiajiao.com/timu3_id_499873[举报]
已知a>0且a≠1,设命题p:函数y=ax+1在R上单调递减,命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点,如果“p∨q”为真,且“p∧q”为假,求a的取值范围.
已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R)其中a∈R
(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a≠![]() 时,求函数f(x)的单调区间与极值.
时,求函数f(x)的单调区间与极值.
已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R),其中a∈R.
(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)当a≠ 时,求函数y=f(x)的单调区间与极值.
时,求函数y=f(x)的单调区间与极值.
 时,求函数f(x)的单调区间与极值.
时,求函数f(x)的单调区间与极值.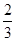 时,求函数y=f(x)的单调区间与极值.
时,求函数y=f(x)的单调区间与极值.