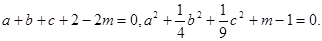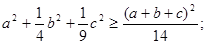摘要:α.β是两个不重合的平面.在α上取4个点.在β上取3个点.则由这些点最多可以确定平面( ). (A)35个 (B)30个 (C)32个 (D)40个 提示:运用排列组合以及平面的性质进行分析.
网址:http://m.1010jiajiao.com/timu3_id_499710[举报]
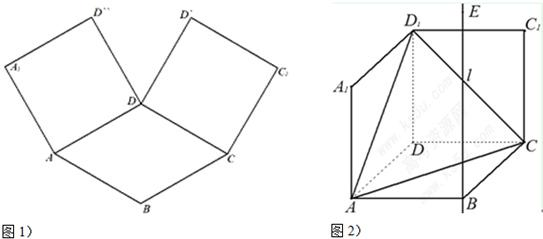
如图1,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADD''A1和CDD'C1都是正方形.将两个正方形分别沿AD,CD折起,使D''与D'重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设BE=t(t>0)(图2).
(1)设二面角E-AC-D1的大小为q,若
≤θ≤
,求t的取值范围;
(2)在线段D1E上是否存在点P,使平面PA1C1∥平面EAC,若存在,求出P分
所成的比λ;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)设二面角E-AC-D1的大小为q,若
| π |
| 4 |
| π |
| 3 |
(2)在线段D1E上是否存在点P,使平面PA1C1∥平面EAC,若存在,求出P分
| D1E |
 查看习题详情和答案>>
查看习题详情和答案>>
本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分
(1)(本小题满分7分)选修4-2:矩阵与变换
变换 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
.
(Ⅰ)求变换 的矩阵;
的矩阵;
(Ⅱ)圆 在变换
在变换 的作用下变成了什么图形?
的作用下变成了什么图形?
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数).
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线 上有一定点
上有一定点 ,曲线
,曲线 与
与 交于M,N两点,求
交于M,N两点,求 的值.
的值.
(3)(本小题满分7分)选修4-5:不等式选讲
已知 为实数,且
为实数,且
(Ⅰ)求证:
(Ⅱ)求实数m的取值范围.
查看习题详情和答案>>
 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
. 在变换
在变换 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数). ,曲线
,曲线 的值.
的值. 为实数,且
为实数,且

 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘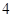 ,变到点
,变到点 .
.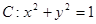 在变换
在变换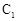 的极坐标方程为:
的极坐标方程为: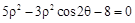 ,直线
,直线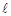 的参数方程为:
的参数方程为: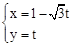 (
(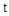 为参数).
为参数).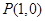 ,曲线
,曲线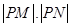 的值.
的值.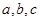 为实数,且
为实数,且