摘要:函数满足..且时., (Ⅰ)设.求数列的通项, (Ⅱ)证明当.时., (Ⅲ)判断的单调性.并证明.
网址:http://m.1010jiajiao.com/timu3_id_499559[举报]
(本题满分14分)设直线![]() . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有![]() . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数![]() .求证:
.求证:![]() 为曲线
为曲线![]() 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
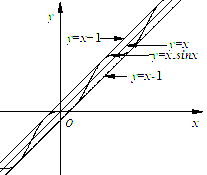

根据上图,试推测曲线![]() 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
(本题满分14分)已知函数f(x)满足2ax·f(x)=2f(x)-1,f(1)=1,设无穷数列{an}满足an+1=f(an).(1)求函数f(x)的表达式;(2)若a1=3,从第几项起,数列{an}中的项满足an<an+1;(3)若![]() <a1<
<a1<![]() (m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 .
.
(1)求方程 的解集;
的解集;
(2)如果△ 的三边
的三边 ,
, ,
, 满足
满足 ,且边
,且边 所对的角为
所对的角为 ,求角
,求角 的取值范围及此时函数
的取值范围及此时函数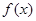 的值域.
的值域.
查看习题详情和答案>>
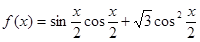 .
.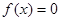 的解集;
的解集;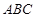 的三边
的三边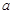 ,
,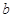 ,
,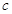 满足
满足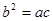 ,且边
,且边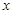 ,求角
,求角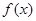 的值域.
的值域.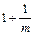 <a1<
<a1<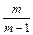 (m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。