摘要:12.(理)已知是定义在上的函数.且满足. ..则 . (文)已知是定义在上的奇函数.且以为周期.若.. 则实数的取值范围是 . 二.选择题本大题共有4题.每题都给出 代号为A.B.C.D的四个结论.其中有且只有一个结论 是正确的.必须把正确结论的代号写在题后的圆括号内. 选对得4分.不选.选错或者选出的代号超过一个(不论 是否都写在圆括号内).一律得零分.
网址:http://m.1010jiajiao.com/timu3_id_499340[举报]
已知 是定义在
是定义在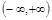 上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足
上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足 .
.
(1)求f (1)、f (-1)的值;
(2)判断f (x)的奇偶性,并说明理由;
(3)证明: (
( 为不为零的常数)
为不为零的常数)
查看习题详情和答案>>
已知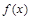 是定义在
是定义在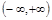 上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足
上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足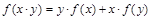 .
.
(1)求f (1)、f (-1)的值;
(2)判断f (x)的奇偶性,并说明理由;
(3)证明: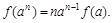 (
(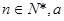 为不为零的常数)
为不为零的常数)
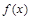 是定义在
是定义在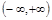 上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足
上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足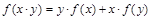 .
.(1)求f (1)、f (-1)的值;
(2)判断f (x)的奇偶性,并说明理由;
(3)证明:
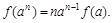 (
(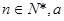 为不为零的常数)
为不为零的常数)若定义在 上的函数
上的函数 满足条件:存在实数
满足条件:存在实数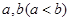 且
且

 ,使得:
,使得:
⑴ 任取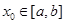 ,有
,有 (
( 是常数);
是常数);
⑵ 对于 内任意
内任意 ,当
,当 ,总有
,总有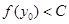 。
。
我们将满足上述两条件的函数 称为“平顶型”函数,称
称为“平顶型”函数,称 为“平顶高度”,称
为“平顶高度”,称 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题:
(1)函数 是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
(2) 已知 是“平顶型”函数,求出
是“平顶型”函数,求出 的值。
的值。
(3)对于(2)中的函数 ,若
,若 在
在 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。
查看习题详情和答案>>
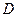 上的函数
上的函数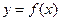
 满足条件:存在实数
满足条件:存在实数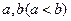 且
且

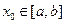 ,有
,有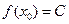 (
(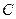 是常数);
是常数); ,当
,当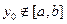 ,总有
,总有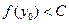 。
。 称为“平顶型”函数,称
称为“平顶型”函数,称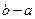 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题: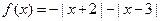 是否为“平顶型”函
是否为“平顶型”函 数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。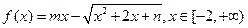 是“平顶型”函数,求出
是“平顶型”函数,求出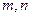 的值。
的值。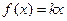 在
在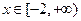 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。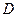 上的函数
上的函数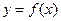
 满足条件:存在实数
满足条件:存在实数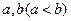 且
且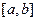

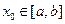 ,有
,有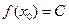 (
(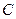 是常数);
是常数);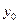 ,当
,当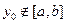 ,总有
,总有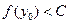 。
。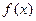 称为“平顶型”函数,称
称为“平顶型”函数,称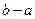 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题: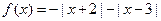 是否为“平顶型”函
是否为“平顶型”函 数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。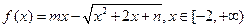 是“平顶型”函数,求出
是“平顶型”函数,求出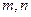 的值。
的值。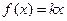 在
在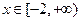 上有两个不相等的根,求实数
上有两个不相等的根,求实数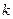 的取值范围。
的取值范围。