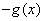题目内容
若定义在 上的函数
上的函数 满足条件:存在实数
满足条件:存在实数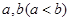 且
且

 ,使得:
,使得:
⑴ 任取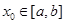 ,有
,有 (
( 是常数);
是常数);
⑵ 对于 内任意
内任意 ,当
,当 ,总有
,总有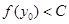 。
。
我们将满足上述两条件的函数 称为“平顶型”函数,称
称为“平顶型”函数,称 为“平顶高度”,称
为“平顶高度”,称 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题:
(1)函数 是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
(2) 已知 是“平顶型”函数,求出
是“平顶型”函数,求出 的值。
的值。
(3)对于(2)中的函数 ,若
,若 在
在 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。
【答案】
解:⑴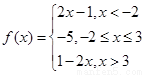 ,
,
则存在区间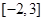 使
使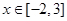 时
时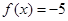
且当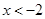 和
和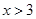 时,
时, 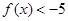 恒成立。
恒成立。
所以函数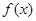 是
“平顶型”函数,平顶高度为
是
“平顶型”函数,平顶高度为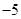 ,平顶宽度为
,平顶宽度为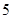 。
。
⑵ 存在区间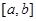

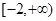 ,使得
,使得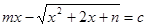 恒成立
恒成立
则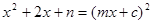 恒成立,则
恒成立,则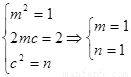 或
或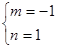
当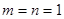 时,
时,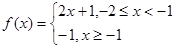 不是“平顶型”函数。
不是“平顶型”函数。
当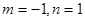 时,
时,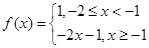 是“平顶型”函数
是“平顶型”函数
⑶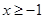 时,
时,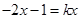 ,则
,则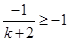 ,得
,得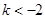 或
或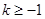
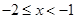 时,
时,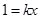 ,则
,则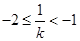 ,得
,得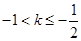
所以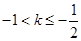 。
。
【解析】略

练习册系列答案
相关题目
 上的函数
上的函数 满足
满足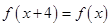 ,且当
,且当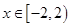 时,
时, ,函数
,函数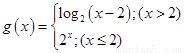 ,则函数
,则函数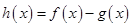 在区间
在区间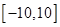 内零点个数是( )
内零点个数是( ) .
.
 .
.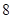
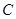 .
.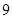
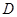 .
.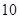
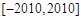 上的函数
上的函数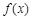 满足:对于任意
满足:对于任意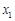 ,
, ,有
,有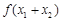
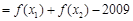 .设
.设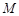 ,
, ,则
,则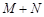 的值为(
)
的值为(
)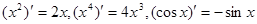 。由归纳推理可得,
。由归纳推理可得,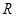 上的函数
上的函数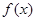 满足
满足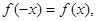 记
记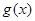 为
为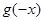 等于
( )
等于
( )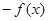 C.
C.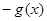
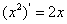 ,
,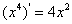 ,
,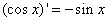 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在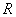 上的函数
上的函数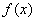 满足
满足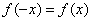 ,记
,记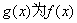 的导函数,则
的导函数,则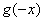
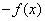 (C)
(C) (D)
(D)