题目内容
已知
是定义在
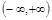上的不恒为零的函数，且对定义域内的任意x, y, f (x)都满足
．
（1）求f (1)、f (-1)的值；
（2）判断f (x)的奇偶性，并说明理由；
（3）证明:
（
为不为零的常数）
【答案】
（1）∴f (1)=0 ；f (－1)=0．（2）函数
是
上的奇函数．
【解析】本试题主要是考查了函数的奇偶性和函数的赋值法思想的运用。
（1）根据已知条件，对于x,y赋值得到结论。令x=y=1时，有
（2）∵f(x)对任意x，y都有
∴令x=t，y=－1,有
将
代入得
（3）对于难以用一般方法证明的自然数命题用数学归纳法证明即可
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
是定义在
上的不恒为零的函数，且对任意的
都满足：
，若
，
（
），求证：
．
（其中
）是偶函数，则实数
；
既是奇函数又是偶函数；
的减区间是
；
是定义在
上的不恒为零的函数，且对任意的
都满足
，则
是定义在
上的不恒为零的函数，且对任意
满足下列关系式：
，
，
，
；
②
为等比数列； 
为等差数列。其中正确的结论是：_____ __。（将所有正确命题的序号都填上）
是定义在
上的不恒为零的函数，且对任意
满足下列关系式：
，
，
，
，考察下列结论：①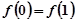
，②
为等比数列 ，④数列
为等差数列，其中正确的结论有_