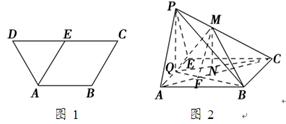
摘要:如图(1).等腰梯形ABCD中.AD∥BC.AB=AD.∠ABC=60°.E是BC的中点.如图(2).将△ABE沿AE折起.使二面角B-AE-C成直二面角.连接BC.BD.F是CD的中点.P是棱BC的中点. (1)求证:AE⊥BD, (2)求证:平面PEF⊥平面AECD, (3)判断DE能否垂直于平面ABC?并说明理由. 分析:由条件可知△ABE为正三角形.要证AE⊥BD.可证明AE垂直于BD所在的平面BDM.即证AE⊥平面BDM,可用判定定理证明平面PEF⊥平面AECD,对于第(3)问可采用反证法证明. 解: (1)证明:取AE中点M.连接BM.DM. ∵在等腰梯形ABCD中.AD∥BC.AB=AD.∠ABC=60°.E是BC的中点. △ABE与△ADE都是等边三角形. ∴BM⊥AE.DM⊥AE. ∵BM∩DM=M.BM.DM⊂平面BDM. ∴AE⊥平面BDM. ∵BD⊂平面BDM.∴AE⊥BD. (2)证明:连接CM.EF交于点N.连接PN.如图. ∵ME∥FC.且ME=FC. ∴四边形MECF是平行四边形. ∴N是线段CM的中点. ∵P是线段BC的中点.∴PN∥BM. ∵BM⊥平面AECD.∴PN⊥平面AECD. 又∵PN⊂平面PEF. ∴平面PEF⊥平面AECD. (3)DE与平面ABC不垂直. 证明:假设DE⊥平面ABC.则DE⊥AB. ∵BM⊥平面AECD.∴BM⊥DE. ∵AB∩BM=B.AB.BM⊂平面ABE. ∴DE⊥平面ABE. ∴DE⊥AE.这与∠AED=60°矛盾. ∴DE与平面ABC不垂直. 评析:翻折与展开是一个问题的两个方面.不论是翻折还是展开.均要注意平面图形与立体图形中各个对应元素的相对变化.元素间大小与位置关系.哪些不变.哪些变化.这是至关重要的.
网址:http://m.1010jiajiao.com/timu3_id_497647[举报]
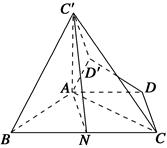
在等腰梯形ABCD中,AD∥BC,AD=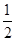 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).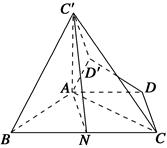
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
在等腰梯形ABCD中,AD∥BC,AD=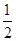 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.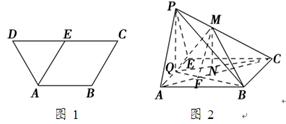
(1)若PA∥平面MQB,求PM∶MC;
(2)若平面AEP⊥平面ABCE,点M是PC的中点,求三棱锥AMQB的体积.