��Ŀ����
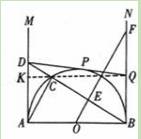
��2011•Ϋ������ͼ��AB�ǰ뾶O��ֱ����AB=2������AM��BNΪ��ԲO�����ߣ���AM��ȡһ��D������BD����Բ�ڵ�C������AC����O����BC�Ĵ���OE������Ϊ��E����BN�ཻ�ڵ�F����D������ԲO������DP���е�ΪP����BN�ཻ�ڵ�Q��
��1����֤����ABC�ס�OFB��
��2������ABD���BFO���������ʱ����BQ�ij���
��3����֤����D��AM���ƶ�ʱ��A����⣩����Qʼ�����߶�BF���е㣮
֤������1����ABΪֱ����
���ACB=90�㣬����AC��BC��
��OE��BC��
��OE��AC��
���BAC=��FOB��
��BN�ǰ�Բ�����ߣ�
���BCA=��FBO=90�㣬
���ACB�ס�OBF��
�⣺��2���ɡ�ACB�ס�OBF�ã���OFB=��DBA����DAB=��OBF=90�㣬
���ABD�ס�BFO��
����ABD���BFO��������ʱ����ABD�ա�BFO��
��AD=1��
��DPQ�ǰ�ԲO�����ߣ�
��OP=1����OP��DP��
��DQ��AB��
��BQ=AD=1
��3���ɣ�2��֪����ABD�ס�BFO��
�� =
= ��
��
��BF= ��
��
��DPQ�ǰ�ԲO�����ߣ�
��AD=DP��QB=BQ��
��Q����AM�Ĵ���QK������ΪK����ֱ��������DQK�У�
DQ2=QK2+DK2��
�ࣨAD+BQ��2=��AD��BQ��2+22��
��BQ= ��
��
��BF=2BQ��
��QΪBF���е㣮
����

 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| A��17�� | B��32�� |
| C��49�� | D��80�� |



 ��x+m����x��3m��ͼ��Ķ���ΪM��ͼ��x����A��B���㣬��y����������D�㣮��ABΪֱ����Բ��Բ��ΪC������E������Ϊ����3��0��������ED����m��0��
��x+m����x��3m��ͼ��Ķ���ΪM��ͼ��x����A��B���㣬��y����������D�㣮��ABΪֱ����Բ��Բ��ΪC������E������Ϊ����3��0��������ED����m��0��