题目内容
如图,AB是半圆O的直径,C是半径OA上一点,PC⊥AB,点D是半圆上位于PC右侧的一点,连接AD交线 段PC于点E,且PD=PE.
段PC于点E,且PD=PE.(1)求证:PD是⊙O的切线;
(2)若⊙O的半径为4,PC=8,设OC=x,PD2=y.
①求y关于x的函数关系式;
②当x=1时,求tan∠BAD的值.
分析:(1)D要证明PD是⊙O的切线,只需证明OD和PD垂直即可.
(2)设PC与⊙O交于F点,连接OF,根据勾股定理求得CF,PF的值,再根据切割线定理求出函数关系式,从而不难求得tan∠BAD的值.
(2)设PC与⊙O交于F点,连接OF,根据勾股定理求得CF,PF的值,再根据切割线定理求出函数关系式,从而不难求得tan∠BAD的值.
解答: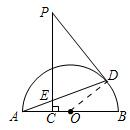 (1)证明:连接OD,则∠OAE=∠ODE,
(1)证明:连接OD,则∠OAE=∠ODE,
∵PC⊥AB,
∴∠OAE+∠CEA=90°.
∵PD=PE,
∴∠CEA=∠PED=∠PDE.
∴∠ODE+∠PDE=90°.
即PD是⊙O的切线.
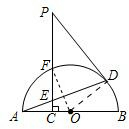 (2)解:①设PC与⊙O交于F点,连接OF,
(2)解:①设PC与⊙O交于F点,连接OF,
∵PC⊥AB,
∴在Rt△CFO中,CF=
.
∵⊙O的半径为4,OC=x,
∴CF=
.
∵PD2=(8+
)(8-
)=48+x2
∴y=x2+48.
②当x=1时,y=49,即PD=PE=7,OC=1,
∴EC=1,AC=3.
∴tan∠BAD=
=
.
 (1)证明:连接OD,则∠OAE=∠ODE,
(1)证明:连接OD,则∠OAE=∠ODE,∵PC⊥AB,
∴∠OAE+∠CEA=90°.
∵PD=PE,
∴∠CEA=∠PED=∠PDE.
∴∠ODE+∠PDE=90°.
即PD是⊙O的切线.
 (2)解:①设PC与⊙O交于F点,连接OF,
(2)解:①设PC与⊙O交于F点,连接OF,∵PC⊥AB,
∴在Rt△CFO中,CF=
| OF2-OC2 |
∵⊙O的半径为4,OC=x,
∴CF=
| 16-x2 |
∵PD2=(8+
| 16-x2 |
| 16-x2 |
∴y=x2+48.
②当x=1时,y=49,即PD=PE=7,OC=1,
∴EC=1,AC=3.
∴tan∠BAD=
| EC |
| AC |
| 1 |
| 3 |
点评:此题考查了切线的判定以及切割线定理等知识点的综合运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
