题目内容
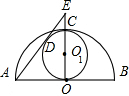如图，AB是半圆O的直径，半径OC⊥AB，⊙O1的直径是OC，AD切⊙O1于D，交OC的延长线于E，设⊙O1的半径为r=3，则DE=分析：先连接O1D，设DE=x，由于OC⊥AB，AE是切线，可知∠AOE=∠O1DE=90°，结合∠E=∠E，易证△AOE∽△O1DE，利用勾股定理可求O1E，进而可求OE，利用相似三角形得出的比例线段，可得x：3=（
+3）：6，求解即可．
| x2+9 |
解答：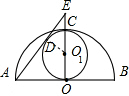
解：如右图所示，连接O1D，设DE=x，
∵OC⊥AB，AE是切线，
∴∠AOE=∠O1DE=90°，
∵∠E=∠E，
∴△AOE∽△O1DE，
∴DE：O1D=OE：AO，
∴x：3=（
+3）：6，
解得x1=0（不合题意，舍去），x2=4．
故答案是4．
解：如右图所示，连接O1D，设DE=x，∵OC⊥AB，AE是切线，
∴∠AOE=∠O1DE=90°，
∵∠E=∠E，
∴△AOE∽△O1DE，
∴DE：O1D=OE：AO，
∴x：3=（
| x2+9 |
解得x1=0（不合题意，舍去），x2=4．
故答案是4．
点评：本题考查了切线的性质、相似三角形的判定和性质、勾股定理、解方程．解题的关键是证明△AOE∽△O1DE．
练习册系列答案
金钥匙试卷系列答案
相关题目
如图，AB是半圆O的直径，AC是弦，点P从点B开始沿BA边向点A以1cm/s的速度移动，若AB长为10cm，点O到AC的距离为4cm．
已知：如图，AB是半圆O的直径，OD是半径，BM切半圆于点B，OC与弦AD平行交BM于点C．
如图，AB是半圆O的直径，点D是半圆上一动点，AB=10，AC=8，当△ACD是等腰三角形时，点D到AB的距离是
如图，AB是半圆O的直径，以OA为直径的半圆O′与弦AC交于点D，O′E∥AC，并交OC于点E，则下列结论：①S△O′OE=
