题目内容
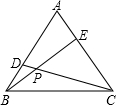 如图,等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD交于点P,若∠ABE:∠CBE=1:2,则∠BDP=
如图,等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD交于点P,若∠ABE:∠CBE=1:2,则∠BDP=分析:根据等边三角形的性质证明△ADC≌△CEB,从而得到∠ACD=∠CBE=40°,然后求∠BDP.
解答:解:∵等边△ABC
∴∠A=∠ABC=∠ACB=60°,AC=BC
∵∠ABE:∠CBE=1:2
∴∠CBE=
∠ABC=40°
又∵AD=CE
∴△ADC≌△CEB(SAS)
∴∠ACD=∠CBE=40°
∴∠BDP=∠BDC=∠A+∠ACD=60°+40°=100°.
故答案为100°.
∴∠A=∠ABC=∠ACB=60°,AC=BC
∵∠ABE:∠CBE=1:2
∴∠CBE=
| 2 |
| 3 |
又∵AD=CE
∴△ADC≌△CEB(SAS)
∴∠ACD=∠CBE=40°
∴∠BDP=∠BDC=∠A+∠ACD=60°+40°=100°.
故答案为100°.
点评:本题利用了:(1)、等边三角形的性质:三边相等,三角等于60度,(2)、全等三角形的判定和性质,(3)、三角形的一个外角等于与它不相邻的两个内角和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF. 如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF. 如图,等边△ABC中,D是BC上一点,以AD为边作等腰△ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°,求∠FDC的度数.
如图,等边△ABC中,D是BC上一点,以AD为边作等腰△ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°,求∠FDC的度数. 如图,等边△ABC中,AD=CE,BD和AE相交于F,BG⊥AE垂足为G,求∠FBG的度数.
如图,等边△ABC中,AD=CE,BD和AE相交于F,BG⊥AE垂足为G,求∠FBG的度数.