题目内容
如图1,△ABC是一张等腰直角三角形彩色纸,AC=BC=50cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.若用这4张纸条为一幅正方形美术作品镶边(纸条不重叠),如图2,则正方形美术作品最大面积是 cm2.

考点:
相似三角形的应用;等腰直角三角形..
分析:
利用相似三角形的性质求出每个纸条的长,将其相加,易得纸片的宽度,从而计算出正方形的边长,从而计算面积即可.
解答:
解:∵△ABC是等腰直角三角形,AC=BC=50cm,如下图所示:
∴AB=50![]() .
.
∴AC•BC=AB•CD,
∴50×50=50![]() •CD,
•CD,
∴CD=25![]() cm,
cm,
于是纸条的宽度为:![]() =5
=5![]() cm,
cm,
∵![]() =,
=,
又AB=50![]() ,
,
∴EF=10![]() .
.
同理,GH=20![]() ,
,
IJ=30![]() ,
,
KL=40![]() ,
,
∴纸条的总长度为:100![]() ,
,
∴图画的正方形的边长为:![]() ﹣5
﹣5![]() =20
=20![]() ,
,
∴面积为(20![]() )2=800cm2.
)2=800cm2.
故答案为:800.

点评:
此题考查了相似三角形的应用,不仅要计算出纸条的长度,还要计算出宽度,要仔细观察图形,寻找隐含条件.

练习册系列答案
相关题目
 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).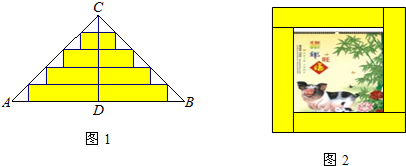

 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).