题目内容
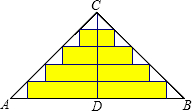 如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和
如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和160
160
cm2.若将这个等腰直角三角形的斜边上的高n等分,那么这些n-1个小长方形的面积和是200-
| 200 |
| n |
200-
cm2.| 200 |
| n |
分析:(1)利用相似三角形的性质求出每个纸条的长,将其相加,易得纸片的宽度,从而计算出问题1的结果;
(2)根据(1)得出的方法,即可推出(n-1)张纸条的面积和.
(2)根据(1)得出的方法,即可推出(n-1)张纸条的面积和.
解答: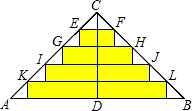 解:(1)∵△ABC是等腰直角三角形,AC=BC=20cm,如下图所示:
解:(1)∵△ABC是等腰直角三角形,AC=BC=20cm,如下图所示:
∴AB=20
.
∴
AC•BC=
AB•CD,
∴20×20=20
•CD,
∴CD=10
(cm),
于是纸条的宽度为:
=2
(cm),
∵
=
,
又∵AB=20
,
∴EF=4
.
同理,GH=8
,
IJ=12
,
KL=16
.
∴4张纸条的面积为:(4
+8
+12
+16
)×2
=160(cm2).
故答案为:160;
(2)由(1)中规律,(n-1)张纸条的面积和为:
20×20÷2-
×
×n÷2
=(200-
)cm2.
故答案为:(200-
).
 解:(1)∵△ABC是等腰直角三角形,AC=BC=20cm,如下图所示:
解:(1)∵△ABC是等腰直角三角形,AC=BC=20cm,如下图所示:∴AB=20
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴20×20=20
| 2 |
∴CD=10
| 2 |
于是纸条的宽度为:
10
| ||
| 5 |
| 2 |
∵
| EF |
| AB |
| 1 |
| 5 |
又∵AB=20
| 2 |
∴EF=4
| 2 |
同理,GH=8
| 2 |
IJ=12
| 2 |
KL=16
| 2 |
∴4张纸条的面积为:(4
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:160;
(2)由(1)中规律,(n-1)张纸条的面积和为:
20×20÷2-
| 20 |
| n |
| 20 |
| n |
=(200-
| 200 |
| n |
故答案为:(200-
| 200 |
| n |
点评:此题考查了相似三角形的应用,不仅要计算出纸条的长度,还要总结出规律,要仔细观察图形,寻找隐含条件.

练习册系列答案
相关题目
 如图,在一张长方形纸条上画一条截线AB,将纸条沿截线AB折叠,则△ABC一定是( )
如图,在一张长方形纸条上画一条截线AB,将纸条沿截线AB折叠,则△ABC一定是( )
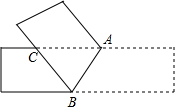 如图,在一张长方形纸条上画一条截线AB,将纸条沿截线AB折叠,则△ABC一定是
如图,在一张长方形纸条上画一条截线AB,将纸条沿截线AB折叠,则△ABC一定是