题目内容
 (2005•遵义)如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且AE⊥AF,A为垂足.
(2005•遵义)如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且AE⊥AF,A为垂足.求证:△AEF是等腰直角三角形.
分析:根据条件可以得出AD=AB,∠ABF=∠ADE=90°,从而可以得出△ABF≌△ADE,就可以得出AF=AE,就可以得出结论.
解答:证明:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠D=∠BAD=90°
∴∠ABF=90°.
∵AE⊥AF,
∴∠FAE=90°.
∴∠FAE=∠BAD,
∴∠FAE-∠BAE=∠BAD-∠BAE,
即∠BAF=∠DAE.
∵在△BAF和△DAE中,
,
∴△BAF≌△DAE(ASA),
∴AF=AE.
∴△AEF是等腰直角三角形.
∴AB=AD,∠ABC=∠D=∠BAD=90°

∴∠ABF=90°.
∵AE⊥AF,
∴∠FAE=90°.
∴∠FAE=∠BAD,
∴∠FAE-∠BAE=∠BAD-∠BAE,
即∠BAF=∠DAE.
∵在△BAF和△DAE中,
|
∴△BAF≌△DAE(ASA),
∴AF=AE.
∴△AEF是等腰直角三角形.
点评:本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,等腰直角三角形的判定,在解答本题时,证明三角形全等是关键.

练习册系列答案
相关题目
 (2005•遵义)如图,把一个边长为6cm的正三角形剪成一个最大的正六边形,则这个正六边形的周长为
(2005•遵义)如图,把一个边长为6cm的正三角形剪成一个最大的正六边形,则这个正六边形的周长为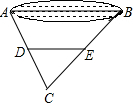 (2005•遵义)如图,A、B两点表示位于一池塘两端的两棵树,为了测量A、B两点间的距离,某同学先在地面上取一个可以直接到达A、B点C,确定AC、BC的中点D、E,并测得DE的长是15米,则A、B的距离为( )
(2005•遵义)如图,A、B两点表示位于一池塘两端的两棵树,为了测量A、B两点间的距离,某同学先在地面上取一个可以直接到达A、B点C,确定AC、BC的中点D、E,并测得DE的长是15米,则A、B的距离为( )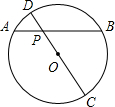 (2005•遵义)如图,⊙O中,弦AB与直径CD相交于点P,且PA=4,PB=6,PD=2,则⊙O的半径为( )
(2005•遵义)如图,⊙O中,弦AB与直径CD相交于点P,且PA=4,PB=6,PD=2,则⊙O的半径为( ) (2005•遵义)如图,在直角坐标系中,经过点A(0,2),B(2,0)和原点O(0,0)三点作⊙C,点P为⊙C上任一点(点P与点O、B不重合),则∠OPB的度数为( )
(2005•遵义)如图,在直角坐标系中,经过点A(0,2),B(2,0)和原点O(0,0)三点作⊙C,点P为⊙C上任一点(点P与点O、B不重合),则∠OPB的度数为( )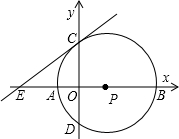 (2005•遵义)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,CD=
(2005•遵义)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,CD=