题目内容
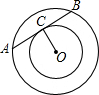如图，以点O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若AB=16，OC=6，则大圆的直径为分析：连接OB，根据切线的性质定理，OC⊥AB；根据垂径定理可求得BC=8，在Rt△OBC中利用勾股定理可求OB=10，即大圆的直径为20．
解答：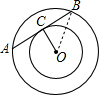
解：连接OB；
∵AB切小圆于点C，
∴OC⊥AB，
∴BC=
AB=
×16=8；
在Rt△OBC中，
OB=
=
=10，
∴大圆的直径为20．
解：连接OB；∵AB切小圆于点C，
∴OC⊥AB，
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OBC中，
OB=
| OC2+CB2 |
| 62+82 |
∴大圆的直径为20．
点评：通过一道题将垂径定理和切割线定理和勾股定理结合起来，而且难度不大，是一道好题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
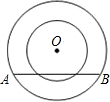如图，以点O为圆心的两个同心圆，半径分别为5和3，若大圆的弦AB与小圆相交，则弦长AB的取值范围是（ ）| A、8≤AB≤10 | B、AB≥8 | C、8＜AB≤10 | D、8＜AB＜10 |
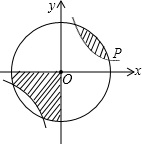如图，以点O为圆心的圆与反比例函数的图象相交，若其中一个交点P的坐标为（5，1），则图中两块阴影部分的面积和为
12、如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标为
如图是以点O为圆心的半圆，AB是半圆的一条弦，延长OB与过点A的直线交于点C，AB=BC=OB．
如图，以点O为圆心的两个同心圆，当大圆的弦AB与小圆相切时弦长AB=8，则这两个同心圆所形成的圆环的面积是