题目内容
（2013•浦东新区二模）如图，已知四边形ABCD是边长为2的菱形，点E、B、C、F都在以O为圆心的同一圆弧上，且∠ADE=∠CDF，那么 |
| EF |
| 4π |
| 3 |
| 4π |
| 3 |
分析：B，C两点恰好落在扇形AEF的
上，即B、C在同一个圆上，连接AC，易证△BDC是等边三角形，即可求得
的圆心角的度数，根据∠ADE=∠CDF可知∠ADC=∠EDF，即可证明
的长=2
，然后利用弧长公式即可求解．
|
| EF |
|
| BC |
|
| EF |
|
| BC |
解答：解：连接BD，
∵菱形ABCD中，DC=BC，
又∵BD=DC，
∴BD=DC=BC，即△DBC是等边三角形．
∴∠BDC=60°，
∴
=
=
，
∵∠ADE=∠CDF，
∴∠ADC=∠EDF，
∵∠ADC=2∠BDC，
∴∠EDF=2∠BDC，
∴
=2
=2×
=
．
∵菱形ABCD中，DC=BC，
又∵BD=DC，
∴BD=DC=BC，即△DBC是等边三角形．
∴∠BDC=60°，
∴
|
| BC |
| 60×2π |
| 180 |
| 2π |
| 3 |
∵∠ADE=∠CDF，
∴∠ADC=∠EDF，
∵∠ADC=2∠BDC，
∴∠EDF=2∠BDC，
∴
|
| EF |
|
| BC |
| 2π |
| 3 |
| 4π |
| 3 |
点评：本题考查了弧长公式，理解B，C两点恰好落在扇形AEF的
上，即B、C在同一个圆上，得到△BDC是等边三角形是关键．
|
| EF |
练习册系列答案
三新快车金牌周周练系列答案
相关题目
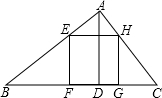（2013•浦东新区一模）如图，已知在△ABC中，边BC=6，高AD=3，正方形EFGH的顶点F、G在边BC上，顶点E、H分别在边AB和AC上，那么这个正方形的边长等于（ ）