摘要：设此抛物线的解析式为: ∵抛物线与轴交于A(1.0).B(两点. ∴ 又∵抛物线与轴交于点C(0.3) ∴. ∴ ∴ 即-----3分用其他解法参照给分 ∴OA=1.OC=3. ∵DC⊥AC.OC⊥轴 ∴△QOC∽△COA ∴.即 ∴OQ=9.--------4分又∵点Q在轴的负半轴上.∴Q( 设直线DC的解析式为:.则解之得: ∴直线DC的解析式为:--------5分 ∵点D是抛物线与直线DC的交点. ∴ 解之得: ∴点D(--------6分用其他解法参照给分 (3)如图.点M为直线上一点.连结AM.PC.PA 设点M(.直线与轴交于点E.∴AE=2 ∵抛物线的顶点为P.对称轴为 ∴P( ∴PE=4 则PM= ∵S四边形AEPC=S四边形OEPC+S△AOC = = =--------7分又∵S四边形AEPC= S△AEP+S△ACP S△AEP= ∴+S△ACP=--------8分 ∵S△MAP=2S△ACP ∴ ∴ ∴.--------9分故抛物线的对称轴上存在点M使S△MAP=2S△ACP 点M(或--------10分用其他解法参照给分二O一一年常州市中考模拟试卷数学试卷

网址：http://m.1010jiajiao.com/timu3_id_495324[举报]

抛物线y=

）x+（k+1）（k为常数）与x轴交于A（x₁，0）、B（x₂，0）（x₁＜0＜x₂）两点，与y轴交于C点，且满足（OA+OB）²=OC²+16．
（1）求此抛物线的解析式；
（2）设M、N是抛物线在x轴上方的两点，且到x轴的距离均为1，点P是抛物线的顶点，问：过M、N、C三点的圆与直线CP是否只有一个公共点C？试证明你的结论．查看习题详情和答案>>

抛物线y= $数学公式$ x²+（k+ $数学公式$ ）x+（k+1）（k为常数）与x轴交于A（x₁，0）、B（x₂，0）（x₁＜0＜x₂）两点，与y轴交于C点，且满足（OA+OB）²=OC²+16．
（1）求此抛物线的解析式；
（2）设M、N是抛物线在x轴上方的两点，且到x轴的距离均为1，点P是抛物线的顶点，问：过M、N、C三点的圆与直线CP是否只有一个公共点C？试证明你的结论．

已知：抛物线y=ax²+bx+c与x轴交于A、B两点，与y轴交于点C．其中点A在x轴的

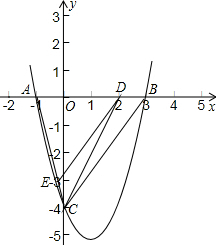负半轴上，点C在y轴的负半轴上，线段OA、OC的长（OA＜OC）是方程x²-5x+4=0的两个根，且抛物线的对称轴是直线x=1．
（1）求A、B、C三点的坐标；
（2）求此抛物线的解析式；
（3）若点D是线段AB上的一个动点（与点A、B不重合），过点D作DE∥BC交AC于点E，连接CD，设BD的长为m，△CDE的面积为S，求S与m的函数关系式，并写出自变量m的取值范围．S是否存在最大值？若存在，求出最大值并求此时D点坐标；若不存在，请说明理由．查看习题详情和答案>>

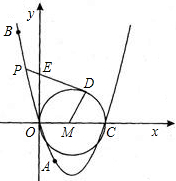已知：抛物线y=ax²+bx+c经过原点（0，0）和A（1，-3），B（-1，5）两点．
（1）求抛物线的解析式；
（2）设抛物线与x轴的另一个交点为C，以OC为直径作⊙M，如果过抛物线上一点P作⊙M的切线PD，切点为D，且与y轴的正半轴交点为E，连接MD，已知E点的坐标为（0，m），求四边形EOMD的面积（用含m的代数式表示）；
（3）延长DM交⊙M于点N，连接ON，OD，当点P在（2）的条件下运动到什么位置时，能使得四边形EOMD和△DON的面积相等，请求出此时点P的坐标．查看习题详情和答案>>

试题分类