题目内容
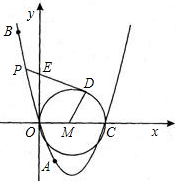 已知:抛物线y=ax2+bx+c经过原点(0,0)和A(1,-3),B(-1,5)两点.
已知:抛物线y=ax2+bx+c经过原点(0,0)和A(1,-3),B(-1,5)两点.(1)求抛物线的解析式;
(2)设抛物线与x轴的另一个交点为C,以OC为直径作⊙M,如果过抛物线上一点P作⊙M的切线PD,切点为D,且与y轴的正半轴交点为E,连接MD,已知E点的坐标为(0,m),求四边形EOMD的面积(用含m的代数式表示);
(3)延长DM交⊙M于点N,连接ON,OD,当点P在(2)的条件下运动到什么位置时,能使得四边形EOMD和△DON的面积相等,请求出此时点P的坐标.
分析:(1)将O、A、B三点坐标代入抛物线的解析式中,即可求出待定系数的值,从而确定抛物线的解析式;
(2)连接EM;由于ED、EO都是⊙M的切线,根据切线长定理可得到ED=EO,根据SSS可证得△EDM≌△EOM,则它们的面积相等,因此四边形EOMD的面积其实是△EOM的面积的2倍,以OM为底,OE为长可求出△EOM的面积,即可得到四边形EOMD的面积表达式;
(3)△DON中,MN=DM,所以△DMO和△OMN等底同高,它们的面积相等;由此可证得△EOM与△OMD的面积相等,由于这两个三角形共用底边OM,则ED∥x轴,根据⊙M的半径即得到直线PD的解析式,联立抛物线的解析式即可求出P点的坐标.
(2)连接EM;由于ED、EO都是⊙M的切线,根据切线长定理可得到ED=EO,根据SSS可证得△EDM≌△EOM,则它们的面积相等,因此四边形EOMD的面积其实是△EOM的面积的2倍,以OM为底,OE为长可求出△EOM的面积,即可得到四边形EOMD的面积表达式;
(3)△DON中,MN=DM,所以△DMO和△OMN等底同高,它们的面积相等;由此可证得△EOM与△OMD的面积相等,由于这两个三角形共用底边OM,则ED∥x轴,根据⊙M的半径即得到直线PD的解析式,联立抛物线的解析式即可求出P点的坐标.
解答:解:(1)∵抛物线过O(0,0),A(1,-3),B(-1,5)三点,
∴
,
解得
;
∴抛物线的解析式为y=x2-4x;
(2)抛物线y=x2-4x与x轴的另一个交点坐标为C(4,0),连接EM;
∴⊙M的半径为2,即OM=DM=2;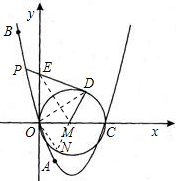
∵ED、EO都是⊙M的切线,
∴EO=ED,△EOM≌△EDM;
∴S四边形EOMD=2S△OME=2×
OM•OE=2m;
(3)延长DM交⊙M于点N,连接ON,OD,EM,
设点D的坐标为(x0,y0),
∵S△DON=2S△DOM=2×
OM×y0=2y0,
当S四边形EOMD=S△DON时,即2m=2y0,m=y0;
∵m=y0,ED∥x轴,
又∵ED为切线,
∴D点的坐标为(2,2);
∵P在直线ED上,故设P点的坐标为(x,2),
∵P在抛物线上,
∴2=x2-4x,
解得x=2±
;
∴P(2+
,2)或P(2-
,2)为所求.
∴
|
解得
|
∴抛物线的解析式为y=x2-4x;
(2)抛物线y=x2-4x与x轴的另一个交点坐标为C(4,0),连接EM;
∴⊙M的半径为2,即OM=DM=2;

∵ED、EO都是⊙M的切线,
∴EO=ED,△EOM≌△EDM;
∴S四边形EOMD=2S△OME=2×
| 1 |
| 2 |
(3)延长DM交⊙M于点N,连接ON,OD,EM,
设点D的坐标为(x0,y0),
∵S△DON=2S△DOM=2×
| 1 |
| 2 |
当S四边形EOMD=S△DON时,即2m=2y0,m=y0;
∵m=y0,ED∥x轴,
又∵ED为切线,
∴D点的坐标为(2,2);
∵P在直线ED上,故设P点的坐标为(x,2),
∵P在抛物线上,
∴2=x2-4x,
解得x=2±
| 6 |
∴P(2+
| 6 |
| 6 |
点评:此题是二次函数与圆的综合题,考查了二次函数解析式的确定、全等三角形的性质、切线长定理、函数图象交点及图形面积的求法等重要知识,能够发现△EOM、△OMD的面积关系,从而得到直线PD与x轴的位置关系是解答(3)题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
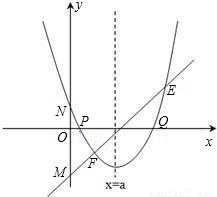
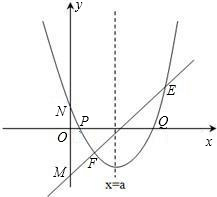 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.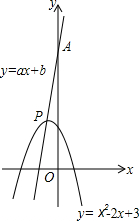 (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.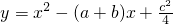 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否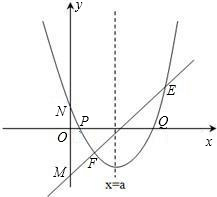 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.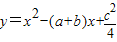 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.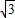 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.