Question

抛物线y=

1

2

x²+（k+

1

2

）x+（k+1）（k为常数）与x轴交于A（x₁，0）、B（x₂，0）（x₁＜0＜x₂）两点，与y轴交于C点，且满足（OA+OB）²=OC²+16．
（1）求此抛物线的解析式；
（2）设M、N是抛物线在x轴上方的两点，且到x轴的距离均为1，点P是抛物线的顶点，问：过M、N、C三点的圆与直线CP是否只有一个公共点C？试证明你的结论．

Answer 1

分析：（1）由（OA+OB）²=OC²+16，可以解得k的值．
（2）由抛物线上的点M、N在x轴上方，且到x轴距离均为1，设MN交y轴于E，求出M、N两点坐标，在Rt△MEC中，MC²=5，同理NC²=20，又∵MN²=25，MN²+MC²=NC²，可证MN是过M、N、C三点的圆的直径，作CF⊥DP于F，连接CD，则CFDE为矩形，在Rt△MEC中和△CDP中，可知即CP²+CD²=DP²，进而证明．

解答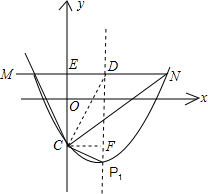：解：（1）∵（OA+OB）²=OC²+16，
∴（-x₁+x₂）²=OC²+16，
∴4（k+

1

2

）²-4×2×（k+1）=（k+1）²+16，
解得k₁=-2，k₂=4．
∵x₁＜0＜x₂，
∴x₁•x₂=2（k+1）＜0，
即k＜-1，
∴k=-2．
∴抛物线解析式为y=

1

2

x²-

3

2

x-1

（2）过M、N、C三点的圆与直线CP只有一个公共点C．证明如下：
如图，∵抛物线上的点M、N在x轴上方，且到x轴距离均为1，设MN交y轴于E，
则M（-1，1），N（4，1），且C（0，-1），P（

3

2

，-

17

8

），
在Rt△MEC中，MC²=5，同理NC²=20，
又∵MN²=25，MN²-MC²=NC²，
∴∠MCN=90°．
故MN是过M、N、C三点的圆的直径，圆心D（

3

2

，1），
作CF⊥DP于F，连接CD，
则CFDE为矩形．
FD=CE=2，CF=ED=

3

2

，
又∵PF=

9

8

，
在Rt△CFP中，CP²=CF²+PF²=（

3

2

）²+（

9

8

）²=

225

64

，
在△CDP中，DP²-CD²=（

25

8

）²-（

5

2

）²=

225

64

=CP²，
即CP²+CD²=DP²，
∴CP⊥CD，直线CP与⊙D相切于点C，
故直线CP和过M、N、C三点的圆只有一个公共点C．

点评：本题二次函数的综合题，要求会求二次函数的解析式和两图象的交点，会判定直线和圆相切，本题步骤有点多，做题需要细心．