��Ŀ����
��֪��������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�A��x���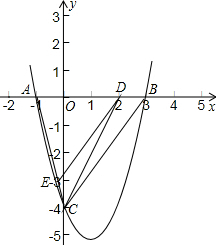 �������ϣ���C��y��ĸ������ϣ��߶�OA��OC�ij���OA��OC���Ƿ���x2-5x+4=0�����������������ߵĶԳ�����ֱ��x=1��
�������ϣ���C��y��ĸ������ϣ��߶�OA��OC�ij���OA��OC���Ƿ���x2-5x+4=0�����������������ߵĶԳ�����ֱ��x=1����1����A��B��C��������ꣻ
��2����������ߵĽ���ʽ��
��3������D���߶�AB�ϵ�һ�����㣨���A��B���غϣ�������D��DE��BC��AC�ڵ�E������CD����BD�ij�Ϊm����CDE�����ΪS����S��m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��S�Ƿ�������ֵ�������ڣ�������ֵ�����ʱD�����ꣻ�������ڣ���˵�����ɣ�
��������1���ⷽ��x2-5x+4=0������������õ�OA��OC�ij��������Եõ�A��C��������꣬��֪�����ߵĶԳ�����x=1��A��Bһ�����ڶԳ���Գƣ����B������Ҳ������Ӧ�����
��2����֪A��B��C��������꣬���ݴ���ϵ�����Ϳ�����������Ľ���ʽ��
��3����֪DE��BC����õ���AED�ס�ACB��AB��AC�ij��ȿ��Ը��ݵ�һ�������AD������m��ʾ�������������������εĶ�Ӧ�ߵı���ȣ��Ϳ������EC�ij�����m��ʾ������DEC���ABC��CE��AC���ϵĸߵıȣ����ǡ�AED�͡�ACB�����Ʊȣ����EC���ϵĸ�Ҳ������m��ʾ��������������ʽ�Ϳ������
S�Ƿ�������ֵ������ת��Ϊ��������ֵ���⣮���ݺ��������ʾͿ��Եõ���
��2����֪A��B��C��������꣬���ݴ���ϵ�����Ϳ�����������Ľ���ʽ��
��3����֪DE��BC����õ���AED�ס�ACB��AB��AC�ij��ȿ��Ը��ݵ�һ�������AD������m��ʾ�������������������εĶ�Ӧ�ߵı���ȣ��Ϳ������EC�ij�����m��ʾ������DEC���ABC��CE��AC���ϵĸߵıȣ����ǡ�AED�͡�ACB�����Ʊȣ����EC���ϵĸ�Ҳ������m��ʾ��������������ʽ�Ϳ������
S�Ƿ�������ֵ������ת��Ϊ��������ֵ���⣮���ݺ��������ʾͿ��Եõ���
����⣺��1����OA��OC�ij���x2-5x+4=0�ĸ���OA��OC��
��OA=1��OC=4��
�ߵ�A��x��ĸ����ᣬ��C��y��ĸ����ᣬ
��A��-1��0��C��0��-4����
��������y=ax2+bx+c�ĶԳ���Ϊx=1��
���ɶԳ��Կɵ�B������Ϊ��3��0����
��A��B��C��������ֱ��ǣ�A��-1��0����B��3��0����C��0��-4����
��2���ߵ�C��0��-4����������y=ax2+bx+cͼ���ϣ�
��c=-4��
��A��-1��0����B��3��0������y=ax2+bx-4��
��
��
��֮��
��
�����������߽���ʽΪ��y=
x2-
x-4��
��3���������⣬BD=m����AD=4-m��
��Rt��OBC��BC=
=5��
��DE��BC��
���ADE�ס�ABC��
��
=
��
��DE=
=
=
��
����E��EF��AB�ڵ�F����sin��EDF=sin��CBA=
=
��
��
=
��
��EF=
DE=
��
=4-m��
��S��CDE=S��ADC-S��ADE=
��4-m����4-
��4-m����4-m��
=-
m2+2m��0��m��4��
��S=-
��m-2��2+2��a=-
��0
�൱m=2ʱ��S�����ֵ2��
���D��������1��0����
��OA=1��OC=4��
�ߵ�A��x��ĸ����ᣬ��C��y��ĸ����ᣬ
��A��-1��0��C��0��-4����
��������y=ax2+bx+c�ĶԳ���Ϊx=1��
���ɶԳ��Կɵ�B������Ϊ��3��0����
��A��B��C��������ֱ��ǣ�A��-1��0����B��3��0����C��0��-4����
��2���ߵ�C��0��-4����������y=ax2+bx+cͼ���ϣ�
��c=-4��
��A��-1��0����B��3��0������y=ax2+bx-4��
��
|
��֮��
|
�����������߽���ʽΪ��y=
| 4 |
| 3 |
| 8 |
| 3 |
��3���������⣬BD=m����AD=4-m��
��Rt��OBC��BC=
| OB2+OC2 |
��DE��BC��
���ADE�ס�ABC��
��
| DE |
| BC |
| AD |
| AB |
��DE=
| AD•BC |
| AB |
| 5(4-m) |
| 4 |
| 20-5m |
| 4 |
����E��EF��AB�ڵ�F����sin��EDF=sin��CBA=
| OC |
| BC |
| 4 |
| 5 |
��
| EF |
| DE |
| 4 |
| 5 |
��EF=
| 4 |
| 5 |
| 4 |
| 5 |
| 20-5m |
| 4 |
��S��CDE=S��ADC-S��ADE=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
��S=-
| 1 |
| 2 |
| 1 |
| 2 |
�൱m=2ʱ��S�����ֵ2��
���D��������1��0����
�����������ۺ������˴���ϵ������������ʽ�����������ε����ʣ��Լ���������ֵ��

��ϰ��ϵ�д�
�����Ŀ
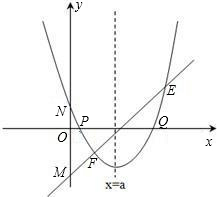 ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�
���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ� ��2013•��������֪��ֱ��y=ax+b��������y=-x2-2x+3�Ķ���P����ͼ��ʾ��
��2013•��������֪��ֱ��y=ax+b��������y=-x2-2x+3�Ķ���P����ͼ��ʾ��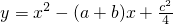 ������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ�
������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ� ����������x�ύ�ڵ�P��Q�����Ƿ�
����������x�ύ�ڵ�P��Q�����Ƿ� ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�
���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ� ������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ�
������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ� ����������x�ύ�ڵ�P��Q�����Ƿ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�
����������x�ύ�ڵ�P��Q�����Ƿ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�