摘要：26．如图1.抛物线与x轴交于A.C两点.与y轴交于B点.与直线交于A.D两点．⑴直接写出A.C两点坐标和直线AD的解析式,⑵如图2.质地均匀的正四面体骰子的各个面上依次标有数字-1.1.3.4．随机抛掷这枚骰子两次.把第一次着地一面的数字m记做P点的横坐标.第二次着地一面的数字n记做P点的纵坐标．则点落在图1中抛物线与直线围成区域内的概率是多少?
网址：http://m.1010jiajiao.com/timu3_id_490003[举报]
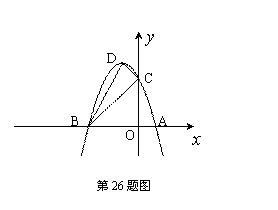
如图，抛物线与
轴交于
(
、
两点，与
轴交于点
(
设抛物线的顶点为
.
（1）求该抛物线的解析式与顶点的坐标.
（2）试判断△
的形状,并说明理由.
（3）探究坐标轴上是否存在点
,使得以
为顶点的三角形与△相似?
若存在,请直接写出点
的坐标；若不存在，请说明理由.
 |
查看习题详情和答案>>
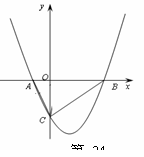
如图，抛物线与
轴交于
、
(6 , 0)两点，且对称轴为直线x = 2，与
轴交于点
。
（1）求抛物线的解析式；
（2）
点
是抛物线对称轴上的一个动点，连接MA、M
C，
当△MAC的周长最小时，求点的坐标；
（3）点
在（1）中抛物线上，点
为抛物线上一
动点，在轴上是否存在点
，使以
为顶点的四边形是平行四边形，如果存在，直接写出所有
满足条件的点的坐标，若不存在，请说明理由。
 |
查看习题详情和答案>>
如图，抛物线与
轴交于
（
，0）、
（
，0）两点，且
，与
轴交于点
，其中
是方程
的两个根。
（1）求抛物线的解析式；
（2）点
是线段
上的一个动点，过点作
∥
，交
于点
，连接
，当
的面积最大时，求点的坐标；
（3）点
在（1）中抛物线上，点
为抛物线上一动点，在轴上是否存在点
，使以
为顶点的四边形是平行四边形，如果存在，求出所有满足条件的点的坐标，若不存在，请说明理由。
轴交于
（
，0）、
（
，0）两点，且
，与
轴交于点
，其中
是方程
的两个根。
是线段
上的一个动点，过点
∥
，交
于点
，连接
，当
的面积最大时，求点
在（1）中抛物线上，点
为抛物线上一动点，在
，使以
为顶点的四边形是平行四边形，如果存在，求出所有满足条件的点
轴交于
（
，0）、
（
，0）两点，且
，与
轴交于点
，其中
是方程
的两个根。（14分）
是线段
上的一个动点，过点
∥
，交
于点
，连接
，当
的面积最大时，求点
在（1）中抛物线上，点
为抛物线上一动点，在
，使以
为顶点的四边形是平行四边形，如果存在，求出所有满足条件的点