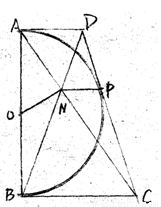
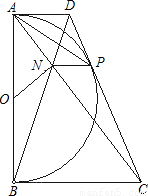
摘要：已知:如图.以定线段AB为直径作半圆O.P为半圆上任意一点.过点P作半圆O的切线分别交过A.B两点的切线于D.C.AC.BD相交于N点.连结ON.NP.下列结论: 四边形ANPD是梯形, ON=NP, DP·PC为定植, PA为∠NPD的平分线. 其中一定成立的是 A.①②③ B.②③④ C.①③④ D.①④ 答案:B
网址：http://m.1010jiajiao.com/timu3_id_488998[举报]
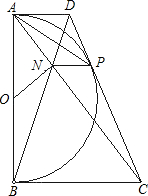已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A、B），过点P作半圆O的切线分别交过A、B两点的切线于D、C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③PA为∠NPD的平分线．其中一定成立的是（ ）| A、①② | B、②③ | C、①③ | D、① |
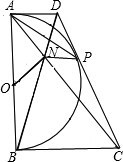已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A，B），过点P作半圆O的切线分别交过A，B两点的切线于D，C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③DP•PC为定值；④PA为∠NPD的平分线．其中一定成立的是（ ）| A、①② | B、②④ | C、①③④ | D、②③④ |
已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A、B），过点P作半圆O的切线分别
交过A、B两点的切线于D、C，连接OC、BP，过点O作OM∥CD分别交BC与BP于点M、N．下列结论：
①S四边形ABCD=
AB•CD；
②AD=AB；
③AD=ON；
④AB为过O、C、D三点的圆的切线．
其中正确的个数有（ ）
交过A、B两点的切线于D、C，连接OC、BP，过点O作OM∥CD分别交BC与BP于点M、N．下列结论：①S四边形ABCD=
| 1 |
| 2 |
②AD=AB；
③AD=ON；
④AB为过O、C、D三点的圆的切线．
其中正确的个数有（ ）
查看习题详情和答案>>
