题目内容
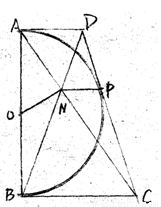
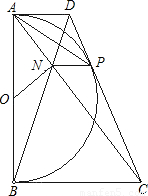
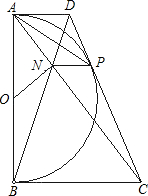
 已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )| A、①② | B、②④ | C、①③④ | D、②③④ |
分析:①由DA,DP,CP,CB为圆O的切线,根据切线性质得到DA与AB垂直,CB与AB垂直,根据同旁内角互补得到AD与BC平行,由两直线平行得到两对内错角相等,进而得到三角形AND与三角形BCN相似,根据相似得比例,等量代换后得到CP:DP=BN:DN,运用比例线段得到NP与BC平行,又BC与AD平行,故NP与AB平行,又DP与AN不平行,根据梯形定义可得ANPD为梯形;
②没有依据;
③连接OP,OD,OC,利用“HL”得到直角三角形AOD与POD全等,同理三角形BOC与三角形POC全等,进而得到对应角相等,由平角定义,利用等量代换得到∠COD为直角,又根据切线性质得到OP与CD垂直,根据两三角形相似得到OP2=DP•PC,而OP为圆O的半径,为定值,故DP•PC为定值;
④由选项①得到的NP与AD平行,得到内错角相等,再根据切线长相等及等边对等角得到一对角相等,等量代换得∠APN=∠APD,故PA为∠NPD的角平分线.
②没有依据;
③连接OP,OD,OC,利用“HL”得到直角三角形AOD与POD全等,同理三角形BOC与三角形POC全等,进而得到对应角相等,由平角定义,利用等量代换得到∠COD为直角,又根据切线性质得到OP与CD垂直,根据两三角形相似得到OP2=DP•PC,而OP为圆O的半径,为定值,故DP•PC为定值;
④由选项①得到的NP与AD平行,得到内错角相等,再根据切线长相等及等边对等角得到一对角相等,等量代换得∠APN=∠APD,故PA为∠NPD的角平分线.
解答:解:①因为DA、DP、CP、CB为⊙O切线,故DA⊥AB,CB⊥AB.
于是AD∥BC,AD=DP,CB=CP.
∴∠CAD=∠NCB,∠ADN=∠DBC,
∴△AND∽△CNB,
∴
=
=
,
∴NP∥BC,
故NP∥AD,又AN与DP相交,
∴四边形ANPD是梯形,本选项正确;
②不能确定;
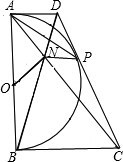
③连接OP,OD,OC,如图所示:
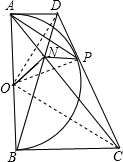
由DA,DP为圆O的切线,
∴∠OAD=∠OPD=90°,
在直角三角形OAD和OPD中,
DA=DP,OD=OD,
∴△OAD≌△OPD,
∴∠AOD=∠POD,
同理∠POC=∠BOC,
∠AOD+∠DOP+∠POC+∠BOC=180°,
∴∠COD=∠DOP+∠COP=90°,又OP⊥CD,
∴∠POD+∠POC=90°,∠POD+∠ODP=90°,
∴∠ODP=∠POC,同理∠POD=∠PCO,
∴△OPD∽△CPO,又AD=DP,CB=CP,
∴
=
,即OP2=DP•PC,
∵OP为圆O的半径,为定值,故DP•PC为定值,本选项正确;
④因为DA=DP,所以∠DAP=∠DPA.
因为NP∥AD,所以∠NPA=∠DAP.
所以∠DPA=∠NPA.
PA为∠NPD的平分线.
则一定成立的选项有:①③④.
故答案为:①③④.
于是AD∥BC,AD=DP,CB=CP.
∴∠CAD=∠NCB,∠ADN=∠DBC,
∴△AND∽△CNB,
∴
| CB |
| AD |
| CN |
| NA |
| CP |
| DP |
∴NP∥BC,
故NP∥AD,又AN与DP相交,
∴四边形ANPD是梯形,本选项正确;
②不能确定;
③连接OP,OD,OC,如图所示:

由DA,DP为圆O的切线,
∴∠OAD=∠OPD=90°,
在直角三角形OAD和OPD中,
DA=DP,OD=OD,
∴△OAD≌△OPD,
∴∠AOD=∠POD,
同理∠POC=∠BOC,
∠AOD+∠DOP+∠POC+∠BOC=180°,
∴∠COD=∠DOP+∠COP=90°,又OP⊥CD,
∴∠POD+∠POC=90°,∠POD+∠ODP=90°,
∴∠ODP=∠POC,同理∠POD=∠PCO,
∴△OPD∽△CPO,又AD=DP,CB=CP,
∴
| OP |
| PC |
| DP |
| OP |
∵OP为圆O的半径,为定值,故DP•PC为定值,本选项正确;
④因为DA=DP,所以∠DAP=∠DPA.
因为NP∥AD,所以∠NPA=∠DAP.
所以∠DPA=∠NPA.
PA为∠NPD的平分线.
则一定成立的选项有:①③④.
故答案为:①③④.
点评:此题难度较大,综合考查了相似三角形的判定与性质,切线的性质及平行线分线段成比例定理,对同学们的推理能力有较高要求.要求学生多观察,多分析,把所学融会贯通,灵活运用,培养了学生分析问题,解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③PA为∠NPD的平分线.其中一定成立的是( )
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③PA为∠NPD的平分线.其中一定成立的是( ) 交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:
交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论: