题目内容
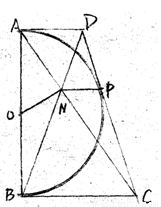
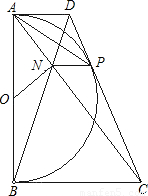
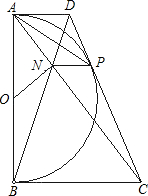已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A、B），过点P作半圆O的切线分别交过A、B两点的切线于D、C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③PA为∠NPD的平分线．其中一定成立的是（ ）| A、①② | B、②③ | C、①③ | D、① |
分析：①根据切线长定理，运用比例线段判断AD∥NP；
②没有依据；
③根据AD=DP，AD∥NP求解．
②没有依据；
③根据AD=DP，AD∥NP求解．
解答：解：①因为DA、DP、CP、CB为⊙O切线，故DA⊥AB，CB⊥AB．
于是AD∥BC，AD=DP，CB=CP．
由于△AND∽△CNB，所以
=
=
，
故NP∥AD，四边形ANPD是梯形；
②不能确定；
③因为DA=DP，所以∠DAP=∠DPA．
因为NP∥AD，所以∠NPA=∠DAP．
所以∠DPA=∠NPA．
PA为∠NPD的平分线．
故选C．
于是AD∥BC，AD=DP，CB=CP．
由于△AND∽△CNB，所以
| CP |
| DP |
| CB |
| AD |
| CN |
| NA |
故NP∥AD，四边形ANPD是梯形；
②不能确定；
③因为DA=DP，所以∠DAP=∠DPA．
因为NP∥AD，所以∠NPA=∠DAP．
所以∠DPA=∠NPA．
PA为∠NPD的平分线．
故选C．
点评：此题难度较大，综合考查了相似三角形的性质，切线的性质及平行线分线段成比例定理，对同学们的推理能力有较高要求．
练习册系列答案
相关题目
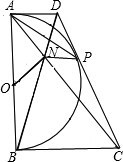已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A，B），过点P作半圆O的切线分别交过A，B两点的切线于D，C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③DP•PC为定值；④PA为∠NPD的平分线．其中一定成立的是（ ）
交过A、B两点的切线于D、C，连接OC、BP，过点O作OM∥CD分别交BC与BP于点M、N．下列结论：
