题目内容
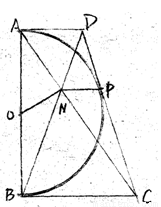
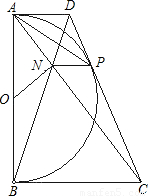
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别 交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:
交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:
①S四边形ABCD=
AB•CD;
②AD=AB;
③AD=ON;
④AB为过O、C、D三点的圆的切线.
其中正确的个数有( )
 交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:
交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:①S四边形ABCD=
| 1 |
| 2 |
②AD=AB;
③AD=ON;
④AB为过O、C、D三点的圆的切线.
其中正确的个数有( )
分析:连接OD、AP,根据切线长定理求出AD=DP,CP=BC,根据面积公式判断①即可;根据直角三角形斜边大于直角边即可判断②;证△DPO和△PON全等证出DP=ON即可判断③,证△DOC是直角三角形,取CD中点Q,证出OQ是半径,证梯形ABCD,推出∠AOQ=90°即可判断④.
解答:解:连接OD、AP,
∵DA、DP、BC分别是圆的切线,切点分别是A、P、B,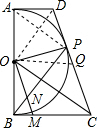
∴DA=DP,CP=CB,∠A=90°=∠B=∠DPO,
∴AD+BC=DP+CP=CD,
∴S四边形ABCD=
(AD+BC)•AB=
AB•CD,∴①正确;
∵AD=DP<OD<AB,∴②错误;
∵AB是圆的直径,
∴∠APB=90°,
∵DP=AD,AO=OP,
∴D、O在AP的垂直平分线上,
∴OD⊥AP,
∵∠DPO=∠APB=90°,
∴∠OPB=∠DPA=∠DOP,
∵OM∥CD,
∴∠POM=∠DPO=90°,
在△DPO和△NOP中
∠PON=∠DPO,OP=OP,∠DOP=∠OPN,
∴△DPO≌△NOP,
∴ON=DP=AD,∴③正确;
∵AP⊥OD,OA=OP,
∴∠AOD=∠POD,
同理∠BOC=∠POC,
∴∠DOC=
×180°=90°,
∴△CDO的外接圆的直径是CD,
∵∠A=∠B=90°,
取CD的中点Q,连接OQ,
∵OA=OB,
∴AD∥OQ∥BC,
∴∠AOQ=90°,
∴④正确.
故选C.
∵DA、DP、BC分别是圆的切线,切点分别是A、P、B,

∴DA=DP,CP=CB,∠A=90°=∠B=∠DPO,
∴AD+BC=DP+CP=CD,
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=DP<OD<AB,∴②错误;
∵AB是圆的直径,
∴∠APB=90°,
∵DP=AD,AO=OP,
∴D、O在AP的垂直平分线上,
∴OD⊥AP,
∵∠DPO=∠APB=90°,
∴∠OPB=∠DPA=∠DOP,
∵OM∥CD,
∴∠POM=∠DPO=90°,
在△DPO和△NOP中
∠PON=∠DPO,OP=OP,∠DOP=∠OPN,
∴△DPO≌△NOP,
∴ON=DP=AD,∴③正确;
∵AP⊥OD,OA=OP,
∴∠AOD=∠POD,
同理∠BOC=∠POC,
∴∠DOC=
| 1 |
| 2 |
∴△CDO的外接圆的直径是CD,
∵∠A=∠B=90°,
取CD的中点Q,连接OQ,
∵OA=OB,
∴AD∥OQ∥BC,
∴∠AOQ=90°,
∴④正确.
故选C.
点评:本题综合考查了切线长定理,全等三角形的性质和判定,直角梯形,圆周角定理,线段的垂直平分线性质,切线的判定等知识点,本题难度较大,对学生有较高的要求,综合性比较强,培养了学生综合运用所学知识分析问题和解决问题的能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
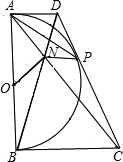 已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )| A、①② | B、②④ | C、①③④ | D、②③④ |
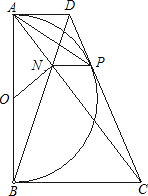 已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③PA为∠NPD的平分线.其中一定成立的是( )
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③PA为∠NPD的平分线.其中一定成立的是( )