摘要:六年级第二学期:第八章 长方体的再认识
网址:http://m.1010jiajiao.com/timu3_id_485332[举报]
 阅读并填空:
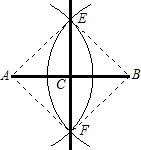
阅读并填空:如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
解:连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(
所以△AEF≌△BEF (
所以∠AEF=∠BEF (
又AE=BE,
所以AC=BC (
即点C是线段AB的中点. 查看习题详情和答案>>
阅读并填空:
如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(______),
______=______(画弧时所取的半径相等),
______=______(画弧时所取的半径相等).
所以△AEF≌△BEF (______).
所以∠AEF=∠BEF (______).
又AE=BE,
所以AC=BC (______).
即点C是线段AB的中点.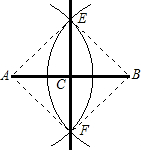
查看习题详情和答案>>
如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(______),
______=______(画弧时所取的半径相等),
______=______(画弧时所取的半径相等).
所以△AEF≌△BEF (______).
所以∠AEF=∠BEF (______).
又AE=BE,
所以AC=BC (______).
即点C是线段AB的中点.

 阅读并填空:
阅读并填空:
如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
解:连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(________),
________=________(画弧时所取的半径相等),
________=________(画弧时所取的半径相等).
所以△AEF≌△BEF (________).
所以∠AEF=∠BEF (________).
又AE=BE,
所以AC=BC (________).
即点C是线段AB的中点.
查看习题详情和答案>>
小明学习了“第八章 幂的运算”后做这样一道题:若(2x-3)x+3=1,求x的值,他解出来的结果为x=1,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?
小明解答过程如下:
解:因为1的任何次幂为1,所以2x-3=1,x=2.且2+3=5
故(2x-3)x+3=(2×2-3)2+3=15=1,所以x=2
你的解答是:
查看习题详情和答案>>
小明解答过程如下:
解:因为1的任何次幂为1,所以2x-3=1,x=2.且2+3=5
故(2x-3)x+3=(2×2-3)2+3=15=1,所以x=2
你的解答是:
解:①∵1的任何次幂为1,所以2x-3=1,x=2.且2+3=5,
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
解:①∵1的任何次幂为1,所以2x-3=1,x=2.且2+3=5,
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
.∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.