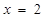题目内容
小明学习了“第八章 幂的运算”后做这样一道题:若(2x-3)x+3=1,求x的值,他解出来的结果为x=1,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?
小明解答过程如下:
解:因为1的任何次幂为1,所以2x-3=1,x=2.且2+3=5
故(2x-3)x+3=(2×2-3)2+3=15=1,所以x=2
你的解答是:
小明解答过程如下:
解:因为1的任何次幂为1,所以2x-3=1,x=2.且2+3=5
故(2x-3)x+3=(2×2-3)2+3=15=1,所以x=2
你的解答是:
解:①∵1的任何次幂为1,所以2x-3=1,x=2.且2+3=5,
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
解:①∵1的任何次幂为1,所以2x-3=1,x=2.且2+3=5,
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
.∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
分析:此题要分三个情况进行讨论:①根据1的任何次幂为1;②根据-1的任何偶次幂也都是1;③任何不是0的数的0次幂也是1,分别求出x的值即可.
解答:解:①∵1的任何次幂为1,所以2x-3=1,x=2.且2+3=5,
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
∴(2x-3)x+3=(2×2-3)2+3=15=1,
∴x=2;
②∵-1的任何偶次幂也都是1,
∴2x-3=-1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x-3≠0,
解的:x=-3,
综上:x=2或3或1.
点评:此题主要考查了有理数的乘方与零次幂,解决问题的关键是要考虑全面所有情况,不要漏解.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
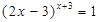 ,求
,求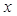 的值,他解出来的结果为
的值,他解出来的结果为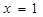 ,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?小明解答过程如下:
,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?小明解答过程如下: 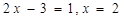 .且
.且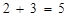
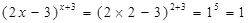 ,所以
,所以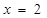
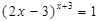 ,求
,求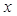 的值,他解出来的结果为
的值,他解出来的结果为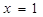 ,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?小明解答过程如下:
,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?小明解答过程如下:
 .且
.且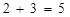
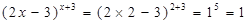 ,所以
,所以