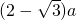摘要:23. 解:(1)证明:在Rt△FCD中. ∵G为DF的中点.∴ CG=FD.---- 1分 同理.在Rt△DEF中. EG=FD. ------2分 ∴ CG=EG.-------3分 中结论仍然成立.即EG=CG.----------4分 证法一:连接AG.过G点作MN⊥AD于M.与EF的延长线交于N点. 在△DAG与△DCG中. ∵ AD=CD.∠ADG=∠CDG.DG=DG. ∴ △DAG≌△DCG. ∴ AG=CG.---------5分 在△DMG与△FNG中. ∵ ∠DGM=∠FGN.FG=DG.∠MDG=∠NFG. ∴ △DMG≌△FNG. ∴ MG=NG 在矩形AENM中.AM=EN. -----6分 在Rt△AMG 与Rt△ENG中. ∵ AM=EN. MG=NG. ∴ △AMG≌△ENG. ∴ AG=EG. ∴ EG=CG. -----------8分 证法二:延长CG至M,使MG=CG. 连接MF.ME.EC. --------4分 在△DCG 与△FMG中. ∵FG=DG.∠MGF=∠CGD.MG=CG. ∴△DCG ≌△FMG. ∴MF=CD.∠FMG=∠DCG. ∴MF∥CD∥AB.---------5分 ∴. 在Rt△MFE 与Rt△CBE中. ∵ MF=CB.EF=BE. ∴△MFE ≌△CBE. ∴.-------------------6分 ∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°. ----7分 ∴ △MEC为直角三角形. ∵ MG = CG. ∴ EG=MC. ∴ .------------8分 中的结论仍然成立. 即EG=CG.其他的结论还有:EG⊥CG.--10分
网址:http://m.1010jiajiao.com/timu3_id_476494[举报]
仿作题.示例:计算tan15°的值.
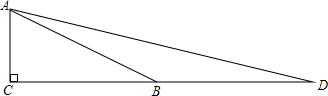
(一)作图
(1)作出Rt△ABC,使∠C=90°,∠ABC=30°;
(2)延长CB到D,使BD=AB;
(二)证明
因为在Rt△ABC中,∠ABC=30°.所以,BD=AB=2a,所以,又∠ADB+∠DAB=∠ABC=30°.
所以∠ADB+∠DAB=
×30°=15°
(三)计算
设AC=a,因为在Rt△ABC中,∠ABC=30°.所以,BD=AB=2a
BC=
=
=
a
所以CD=CB+BD=
a+2a=(2+
)a,所以tan15°=
=
=(2-
)a
问题:请您根据tan15°的计算方法,计算tan22°30′的值.
查看习题详情和答案>>

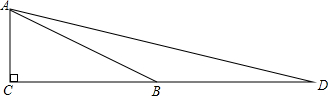
(一)作图
(1)作出Rt△ABC,使∠C=90°,∠ABC=30°;
(2)延长CB到D,使BD=AB;
(二)证明
因为在Rt△ABC中,∠ABC=30°.所以,BD=AB=2a,所以,又∠ADB+∠DAB=∠ABC=30°.
所以∠ADB+∠DAB=
| 1 |
| 2 |
(三)计算
设AC=a,因为在Rt△ABC中,∠ABC=30°.所以,BD=AB=2a
BC=
| AB2-AC2 |
| (2a)2-a2 |
| 3 |
所以CD=CB+BD=
| 3 |
| 3 |
| AC |
| CB |
| a | ||
(2+
|
| 3 |
问题:请您根据tan15°的计算方法,计算tan22°30′的值.
用反证法证明命题“在Rt△ABC中,若∠A=90°,则∠B≤45°或∠C≤45°“时,应先假设( )
| A、∠B>45°,∠C≤45° | B、∠B≤45°,∠C>45° | C、∠B>45°,∠C>45° | D、∠B≤45°,∠C≤45° |
用反证法证明命题“在Rt△ABC中,若∠A=90°,则∠B≤45°或∠C≤45°“时,应先假设()
A. ∠B>45°,∠C≤45° B. ∠B≤45°,∠C>45° C. ∠B>45°,∠C>45° D. ∠B≤45°,∠C≤45°
查看习题详情和答案>>
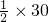 °=15°
°=15° =
=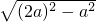 =
=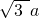
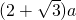 ,所以tan15°=
,所以tan15°= =
=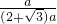 =
=