摘要:28..⊙O1与⊙O2相交于A.B两点.经过A点的直线分别交⊙O1.⊙O2于C.D两点(C.D不与B重合).连结BD.过点C作BD的平行线交⊙O1于点E.连BE. (1)求证:BE是⊙O2的切线, .若两圆圆心在公共弦AB的同侧.其他条件不变.判断BE和⊙O2的位置关系. [提示](1)过B作⊙O2的直径BH.连结AB.AH.证∠EBH=90°.(2)用类似的方法去探求. [证明](1)连结AB.作⊙O2的直径BH.连结AH. 则 ∠ABH+∠H=90°.∠H=∠ADB.∠EBA=∠ECA. ∵ EC∥BD. ∴ ∠ADB=∠ACE=∠EBA. ∴ ∠EBA+∠ABH=90°. 即 ∠EBH=90°. ∴ BE是⊙O2的切线. (2)同理可知.BE仍是⊙O2的切线. [点评]证明一与圆有公共点的直线是圆的切线的一般方法是过公共点作半径.再证直径与半径垂直.但此题已知条件中无90°的角.故作直径构造90°的角.再进行角的转换.同时两圆相交.通常作它们的公共弦.这样把两圆中的角都联系起来了.另外.当问题进行了变式时.要学会借鉴已有的思路解题.
网址:http://m.1010jiajiao.com/timu3_id_459650[举报]
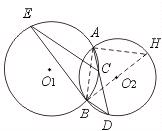 16、已知:如图,⊙O1与⊙O2相交于A、B两点,经过A点的直线分别交⊙O1、⊙O2于C、D两点(C、D不与B重合),连接BD,过点C作BD的平行线交⊙O1于点E,连BE.
16、已知:如图,⊙O1与⊙O2相交于A、B两点,经过A点的直线分别交⊙O1、⊙O2于C、D两点(C、D不与B重合),连接BD,过点C作BD的平行线交⊙O1于点E,连BE.求证:BE是⊙O2的切线;
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.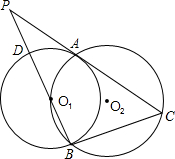 已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P、PB与⊙O1交于点D.
已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P、PB与⊙O1交于点D. 22、已知:如图,⊙O1与⊙O2相交于点A、B,过A的直线分别交两圆于点C、D,G为CD中点,BG分别交两圆于点E、F.求证:EG=FG.
22、已知:如图,⊙O1与⊙O2相交于点A、B,过A的直线分别交两圆于点C、D,G为CD中点,BG分别交两圆于点E、F.求证:EG=FG.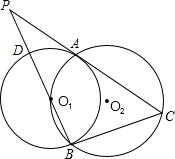 已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P、PB与⊙O1交于点D.
已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P、PB与⊙O1交于点D.