题目内容
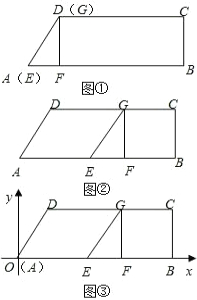 如图①,在梯形ABCD中,CD∥AB,∠ABC=90°,∠DAB=60°,AD=2,CD=4.另有一直角三角形EFG,∠EFG=90°,点G与点D重合,点E与点A重合,点F在AB上,让△EFG的边EF在AB上,点G在DC上,以每秒1个单位的速度沿着AB方向向右运动,如图②,点F与点B重合时停止运动,设运动时间为t秒.
如图①,在梯形ABCD中,CD∥AB,∠ABC=90°,∠DAB=60°,AD=2,CD=4.另有一直角三角形EFG,∠EFG=90°,点G与点D重合,点E与点A重合,点F在AB上,让△EFG的边EF在AB上,点G在DC上,以每秒1个单位的速度沿着AB方向向右运动,如图②,点F与点B重合时停止运动,设运动时间为t秒.(1)在上述运动过程中,请分别写出当四边形FBCG为正方形和四边形AEGD为平行四边形时对应时刻t的值或范围;
(2)以点A为原点,以AB所在直线为x轴,过点A垂直于AB的直线为y轴,建立如图③所示的坐标系.求过A,D,C三点的抛物线的解析式;
(3)探究:延长EG交(2)中的抛物线于点Q,是否存在这样的时刻t使得△ABQ的面积与梯形ABCD的面积相等?若存在,求出t的值;若不存在,请说明理由.
分析:(1)∵∠ABC=90°,∠DAB=60°,AD=2,解直角△DAF可得DF=
,又FB=4-t,当GF=FB时,四边形FBCG为正方形,即
=4-t,G、C重合之前,始终有GE∥OE,DG∥OE,故当0<t≤4时,四边形AEGD为平行四边形;
(2)解直角△EFG得GF=
,EF=1,又AD=2,∴点D、C的坐标分别是(1,
),(5,
),抛物线经过原点,可求抛物线解析式;
(3)梯形ABCD面积可求,△ABQ的底边AB为已知,由此可求AB边上的高,即点Q的纵坐标,根据抛物线解析式求横坐标,进一步求出E点位置,可得出运动时间t.
| 3 |
| 3 |
(2)解直角△EFG得GF=
| 3 |
| 3 |
| 3 |
(3)梯形ABCD面积可求,△ABQ的底边AB为已知,由此可求AB边上的高,即点Q的纵坐标,根据抛物线解析式求横坐标,进一步求出E点位置,可得出运动时间t.
解答:解:(1)∵∠ABC=90°,∠DAB=60°,AD=2,
∴解直角△DAF可得AF=1,DF=
,
当t=4-
时,四边形FBCG为正方形.
当0<t≤4时,四边形AEGD为平行四边形.
(2)点D、C的坐标分别是(1,
),(5,
),
∵抛物线经过原点O(0,0),
∴设抛物线的解析式为y=ax2+bx,
将D、C两点坐标代入得
,
解得
,
∴抛物线的解析式为y=-
x2+
x;
(3)∵点Q在抛物线上,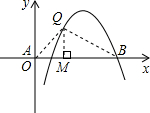
∴点Q(x,-
x2+
x),
过点Q作QM⊥x轴于点M,又B(5,0),
则S△ABQ=
AB•QM=
|-
x2+
x|=
|-
x2+6
x|;
又S四边形ABCD=(4+5)×
×
=
,
令
|-
x2+6
x|=
,
∵EG的延长线与抛物线交于x轴的上方,
∴-x2+6x=9解得x=3,
当x=3时,y=-
×9+
×3=
,
∵∠QEM=60°,
∴EM=
=
÷
=
,
∴t=3-
=
(秒).
即存在这样的时刻t,当t=
秒时,△AQB的面积与梯形ABCD的面积相等.
∴解直角△DAF可得AF=1,DF=
| 3 |
当t=4-
| 3 |
当0<t≤4时,四边形AEGD为平行四边形.
(2)点D、C的坐标分别是(1,
| 3 |
| 3 |
∵抛物线经过原点O(0,0),
∴设抛物线的解析式为y=ax2+bx,
将D、C两点坐标代入得
|
解得
|
∴抛物线的解析式为y=-
| ||
| 5 |
6
| ||
| 5 |
(3)∵点Q在抛物线上,
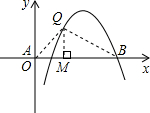
∴点Q(x,-
| ||
| 5 |
6
| ||
| 5 |
过点Q作QM⊥x轴于点M,又B(5,0),
则S△ABQ=
| 1 |
| 2 |
| 5 |
| 2 |
| ||
| 5 |
6
| ||
| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
又S四边形ABCD=(4+5)×
| 3 |
| 1 |
| 2 |
| 9 |
| 2 |
| 3 |
令
| 1 |
| 2 |
| 3 |
| 3 |
| 9 |
| 2 |
| 3 |
∵EG的延长线与抛物线交于x轴的上方,
∴-x2+6x=9解得x=3,
当x=3时,y=-
| ||
| 5 |
6
| ||
| 5 |
| 9 |
| 5 |
| 3 |
∵∠QEM=60°,
∴EM=
| MQ |
| tan60° |
| 9 |
| 5 |
| 3 |
| 3 |
| 9 |
| 5 |
∴t=3-
| 9 |
| 5 |
| 6 |
| 5 |
即存在这样的时刻t,当t=
| 6 |
| 5 |
点评:本题考查了四边形的判定方法,点的坐标及抛物线解析式的求法,并用面积法探讨了一些实际问题,具有较强的综合性.

练习册系列答案
相关题目
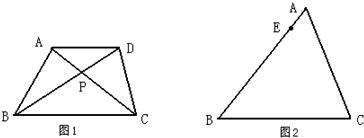

 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是

