摘要：21．如图.已知M.N两点在正方形ABCD的对角线BD上移动.∠MCN为定角a. 连结AM.AN.并延长分别交BC.CD于E.F两点.则∠CME与∠CNF在M. N两点移动过程.它们的和是否有变化?证明你的结论． [提示]BD为正方形ABCD的对称轴. ∴ ∠1＝∠3.∠2＝∠4. 用∠1和∠2表示∠MCN以及∠EMC+∠FNC． [答案]∵ BD为正方形ABCD的对称轴. ∴ ∠1＝∠3.∠2＝∠4. ∴ ∠EMC＝180°-∠1-∠3＝180°-2∠1． 同理 ∠FNC＝180°-2∠2． ∴ ∠EMC+∠FNC＝360°-2． ∵ ∠MCN＝180°-. ∴ ∠EMC+∠FNC总与2∠MCN相等． 因此∠EMC+∠FNC始终为定角.这定角为∠MCN的2倍．
网址：http://m.1010jiajiao.com/timu3_id_455183[举报]
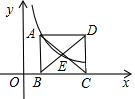如图，已知点（1，3）在函数y=| k |
| x |
| k |
| x |
如图，已知正方形ABCD的边长为4cm，动点P从点B出发，以2cm/s的速度、沿B→C→D方向，向点D运动；动点Q从点A出发，以1cm/s的速度、沿A→B方向，向点B运动．若P、Q两点同时出发，运动时间为t秒．
（1）连接PD、PQ、DQ，设△PQD的面积为S，试求S与t之间的函数关系式；
（2）当点P在BC上运动时，是否存在这样的t，使得△PQD是等腰三角形？若存在，请求出符合条件的t的值；若不存在，请说明理由；
（3）以点P为圆心，作⊙P，使得⊙P与对角线BD相切．问：当点P在CD上运动时，是否存在这样的t，使得⊙P恰好经过正方形ABCD的某一边的中点若存在，请求出符合条件的t的值；若不存在，请说明理由．
查看习题详情和答案>>
（1）连接PD、PQ、DQ，设△PQD的面积为S，试求S与t之间的函数关系式；
（2）当点P在BC上运动时，是否存在这样的t，使得△PQD是等腰三角形？若存在，请求出符合条件的t的值；若不存在，请说明理由；
（3）以点P为圆心，作⊙P，使得⊙P与对角线BD相切．问：当点P在CD上运动时，是否存在这样的t，使得⊙P恰好经过正方形ABCD的某一边的中点若存在，请求出符合条件的t的值；若不存在，请说明理由．
查看习题详情和答案>>
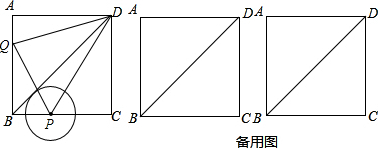
如图，已知一次函数y=x+2的图象分别交x轴、y轴于A、B两点，圆O1过以OB为边长的正方形OBCD的四个顶点，两动点P、Q同时从点A出发在四边形ABCD上运动，其中动点P以每秒
个单位长度的速度沿A→B→C运动后停止，动点Q以每秒2
个单位长度的速度沿A→O→D→C→B运动，AO1交于y轴于E点，P、Q点运动的时间为t（秒）
（1）点E的坐标是
（2）三角形ABE的面积是
；
（3）当Q点运动在线段AD上时，是否存在某一时刻t（秒），使得S△APQ：S△ABE=3：4？若存在，请确定t的值和直线PQ所对应的函数解析式；若不存在，请说明理由？
查看习题详情和答案>>
| 2 |
个单位长度的速度沿A→O→D→C→B运动，AO1交于y轴于E点，P、Q点运动的时间为t（秒）（1）点E的坐标是
（0，
）
| 2 |
| 3 |
（0，
）
；| 2 |
| 3 |
（2）三角形ABE的面积是
| 4 |
| 3 |
| 4 |
| 3 |
（3）当Q点运动在线段AD上时，是否存在某一时刻t（秒），使得S△APQ：S△ABE=3：4？若存在，请确定t的值和直线PQ所对应的函数解析式；若不存在，请说明理由？
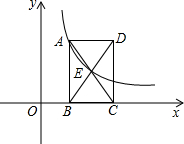如图，已知点（1，2）在函数y=
（x＞0）的图象上，矩形ABCD的边BC在x正半轴上，E是对角线AC、BD的交点，函数y=