ΧβΡΩΡΎ»ί
»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ4cmΘ§Ε·ΒψP¥”ΒψB≥ωΖΔΘ§“‘2cm/sΒΡΥΌΕ»ΓΔ―ΊBΓζCΓζDΖΫœρΘ§œρΒψD‘ΥΕ·ΘΜΕ·ΒψQ¥”ΒψA≥ωΖΔΘ§“‘1cm/sΒΡΥΌΕ»ΓΔ―ΊAΓζBΖΫœρΘ§œρΒψB‘ΥΕ·Θ°»τPΓΔQΝΫΒψΆ§ ±≥ωΖΔΘ§‘ΥΕ· ±ΦδΈΣtΟκΘ°Θ®1Θ©Ν§Ϋ”PDΓΔPQΓΔDQΘ§…ηΓςPQDΒΡΟφΜΐΈΣSΘ§ ‘«σS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©Β±ΒψP‘ΎBC…œ‘ΥΕ· ±Θ§ «Ζώ¥φ‘Ύ’β―υΒΡtΘ§ ΙΒΟΓςPQD «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΖϊΚœΧθΦΰΒΡtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©“‘ΒψPΈΣ‘≤–ΡΘ§ΉςΓ―PΘ§ ΙΒΟΓ―P”κΕ‘Ϋ«œΏBDœύ«–Θ°Έ ΘΚΒ±ΒψP‘ΎCD…œ‘ΥΕ· ±Θ§ «Ζώ¥φ‘Ύ’β―υΒΡtΘ§ ΙΒΟΓ―P«ΓΚΟΨ≠Ιΐ’ΐΖΫ–ΈABCDΒΡΡ≥“Μ±ΏΒΡ÷–Βψ»τ¥φ‘ΎΘ§«κ«σ≥ωΖϊΚœΧθΦΰΒΡtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
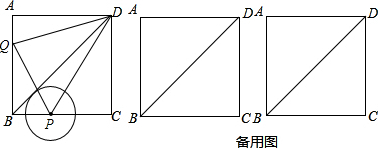
Ζ÷ΈωΘΚΘ®1Θ©Ω…ΗυΨί»ΐΫ«–ΈPQDΒΡΟφΜΐ=Χί–ΈABPDΒΡΟφΜΐ-»ΐΫ«–ΈAQDΒΡΟφΜΐ-»ΐΫ«–ΈBPQΒΡΟφΜΐά¥«σΫβΘ§ΗυΨίPΘ§QΒΡΥΌΕ»Θ§Ω…“‘±μ Ψ≥ωAQΓΔBQΓΔBPΘ§Ρ«Ο¥ΨΆΡή±μ Ψ≥ωΝΫ÷±Ϋ«»ΐΫ«–ΈΒΡ÷±Ϋ«±Ώ“‘ΦΑΧί–ΈΒΡΝΫΒΉΚΆΗΏΘ§Ω…ΗυΨίΗςΉ‘ΒΡΟφΜΐΦΤΥψΙΪ ΫΒΟ≥ωSΓΔt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ°
Θ®2Θ©“ΣΖ÷»ΐ÷÷«ιΩωΫχ––Χ÷¬έΘΚ
Β±PD=QD ±Θ§ΗυΨί–±±Ώ÷±Ϋ«±ΏΕ®άμΘ§Έ“Ο«Ω…ΒΟ≥ω»ΐΫ«–ΈAQDΚΆCPD»ΪΒ»Θ§Ρ«Ο¥Ω…ΒΟ≥ωCP=AQΘ§Ω…”Ο ±ΦδtΖ÷±π±μ Ψ≥ωAQΓΔCPΒΡ≥ΛΘ§»ΜΚσΩ…ΗυΨίΝΫ’ΏΒΡΒ»ΝΩΙΊœΒ«σ≥ωtΒΡ÷ΒΘ°
Β±PD=PQ ±Θ§Ω…‘Ύ÷±Ϋ«»ΐΫ«–ΈBPQΚΆPDC÷–Θ§ΗυΨίΙ¥Ι…Ε®άμΘ§”ΟBQΓΔBP±μ Ψ≥ωPQΘ§”ΟCPΓΔCD±μ Ψ≥ωPDΘΜBQΓΔBPΓΔPCΕΦΩ…“‘”Οtά¥±μ ΨΘ§”…¥ΥΩ…ΒΟ≥ωΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…ΒΟ≥ωtΒΡ÷ΒΘ°
Β±QD=PQ ±Θ§ΖΫΖ®Ά§…œΘ°
Θ®3Θ©”ΠΒ±ΩΦ¬«ΝΫ÷÷«ιΩωΘΚ
ΔΌ‘≤–ΡPΨ≠ΙΐBCΒΡ÷–ΒψΘ§»γΙϊ…η‘≤”κBDœύ«–”ΎMΘ§BCΒΡ÷–Βψ «EΘ§Ρ«Ο¥PM=PEΘ§Ω…”Ο ±Φδt±μ Ψ≥ωCPΒΡ≥ΛΘ§“≤ΨΆΡή±μ Ψ≥ωDPΒΡ≥ΛΘ§Ρ«Ο¥Ω…“‘ΗυΨίΙ¥Ι…Ε®άμ‘Ύ÷±Ϋ«»ΐΫ«–ΈCEP÷–±μ Ψ≥ωPE2ΒΡ≥ΛΘ§“≤ΨΆ±μ Ψ≥ωΝΥPM2ΒΡ≥ΛΘ§»ΜΚσΗυΨίΓœMDPΒΡ’ΐœ“÷Β±μ Ψ≥ωDPΘ§PMΒΡΙΊœΒΘ§”…¥ΥΩ…ΒΟ≥ωΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫχΕχ«σ≥ωtΒΡ÷ΒΘ°
ΔΎ‘≤–ΡPΨ≠ΙΐCDΒΡ÷–ΒψΘ§»γΙΐCDΒΡ÷–Βψ «EΘ§Ρ«Ο¥PM=PEΘ§‘Ύ÷±Ϋ«»ΐΫ«–ΈDMP÷–Θ§DP=2-ΑκΨΕΒΡ≥ΛΘ§PM=ΑκΨΕΒΡ≥ΛΘ§“ρ¥ΥΩ…ΗυΨίΓœMDPΒΡ’ΐœ“Κ· ΐ«σ≥ωΑκΨΕΒΡ≥ΛΘ§»ΜΚσ”Οt±μ Ψ≥ωCPΘ§Φ¥Ω…«σ≥ωtΒΡ÷ΒΘ°
Θ®2Θ©“ΣΖ÷»ΐ÷÷«ιΩωΫχ––Χ÷¬έΘΚ
Β±PD=QD ±Θ§ΗυΨί–±±Ώ÷±Ϋ«±ΏΕ®άμΘ§Έ“Ο«Ω…ΒΟ≥ω»ΐΫ«–ΈAQDΚΆCPD»ΪΒ»Θ§Ρ«Ο¥Ω…ΒΟ≥ωCP=AQΘ§Ω…”Ο ±ΦδtΖ÷±π±μ Ψ≥ωAQΓΔCPΒΡ≥ΛΘ§»ΜΚσΩ…ΗυΨίΝΫ’ΏΒΡΒ»ΝΩΙΊœΒ«σ≥ωtΒΡ÷ΒΘ°
Β±PD=PQ ±Θ§Ω…‘Ύ÷±Ϋ«»ΐΫ«–ΈBPQΚΆPDC÷–Θ§ΗυΨίΙ¥Ι…Ε®άμΘ§”ΟBQΓΔBP±μ Ψ≥ωPQΘ§”ΟCPΓΔCD±μ Ψ≥ωPDΘΜBQΓΔBPΓΔPCΕΦΩ…“‘”Οtά¥±μ ΨΘ§”…¥ΥΩ…ΒΟ≥ωΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…ΒΟ≥ωtΒΡ÷ΒΘ°
Β±QD=PQ ±Θ§ΖΫΖ®Ά§…œΘ°
Θ®3Θ©”ΠΒ±ΩΦ¬«ΝΫ÷÷«ιΩωΘΚ
ΔΌ‘≤–ΡPΨ≠ΙΐBCΒΡ÷–ΒψΘ§»γΙϊ…η‘≤”κBDœύ«–”ΎMΘ§BCΒΡ÷–Βψ «EΘ§Ρ«Ο¥PM=PEΘ§Ω…”Ο ±Φδt±μ Ψ≥ωCPΒΡ≥ΛΘ§“≤ΨΆΡή±μ Ψ≥ωDPΒΡ≥ΛΘ§Ρ«Ο¥Ω…“‘ΗυΨίΙ¥Ι…Ε®άμ‘Ύ÷±Ϋ«»ΐΫ«–ΈCEP÷–±μ Ψ≥ωPE2ΒΡ≥ΛΘ§“≤ΨΆ±μ Ψ≥ωΝΥPM2ΒΡ≥ΛΘ§»ΜΚσΗυΨίΓœMDPΒΡ’ΐœ“÷Β±μ Ψ≥ωDPΘ§PMΒΡΙΊœΒΘ§”…¥ΥΩ…ΒΟ≥ωΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫχΕχ«σ≥ωtΒΡ÷ΒΘ°
ΔΎ‘≤–ΡPΨ≠ΙΐCDΒΡ÷–ΒψΘ§»γΙΐCDΒΡ÷–Βψ «EΘ§Ρ«Ο¥PM=PEΘ§‘Ύ÷±Ϋ«»ΐΫ«–ΈDMP÷–Θ§DP=2-ΑκΨΕΒΡ≥ΛΘ§PM=ΑκΨΕΒΡ≥ΛΘ§“ρ¥ΥΩ…ΗυΨίΓœMDPΒΡ’ΐœ“Κ· ΐ«σ≥ωΑκΨΕΒΡ≥ΛΘ§»ΜΚσ”Οt±μ Ψ≥ωCPΘ§Φ¥Ω…«σ≥ωtΒΡ÷ΒΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©Β±0ΓήtΓή2 ±Θ§Φ¥ΒψP‘ΎBC…œ ±Θ§
S=S’ΐΖΫ–ΈABCD-SΓςADQ-SΓςBPQ-SΓςPCD=16-
•4•t-
•2t•Θ®4-tΘ©-
•Θ®4-2tΘ©•4=t2-2t+8Θ§
Β±2ΘΦtΓή4 ±Θ§Φ¥ΒψP‘ΎCD…œ ±Θ§DP=8-2tΘ§
S=
•Θ®8-2tΘ©•4=16-4tΘ°
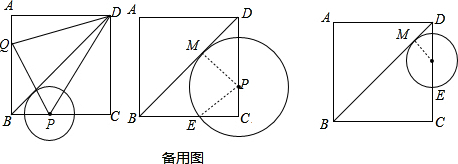
Θ®2Θ©ΔΌ»τPD=QDΘ§‘ρRtΓςDCPΓ’RtΓςDAQΘ®HLΘ©Θ°
ΓύCP=AQΘ°Φ¥t=4-2tΘ§ΫβΒΟt=
Θ°
ΔΎ»τPD=PQΘ§‘ρPD2=PQ2Θ§Φ¥42+Θ®4-2tΘ©2=Θ®4-tΘ©2+Θ®2tΘ©2Θ°
ΫβΒΟt=-4Γά4
Θ§Τδ÷–t=-4-4
ΘΦ0≤ΜΚœΧβ“βΘ§…α»ΞΘ§Γύt=-4+4
Θ°
Δέ»τQD=PQΘ§‘ρQD2=PQ2Θ§Φ¥16+t2=Θ®4-tΘ©2+Θ®2tΘ©2Θ§ΫβΒΟt=0Μρt=2Θ§
Γύt=
Μρt=-4+4
Μρt=0Μρt=2 ±Θ§ΓςPQD «Β»―ϋ»ΐΫ«–ΈΘ°
Θ®3Θ©Β±P‘ΎCD…œ‘ΥΕ· ±Θ§»τΓ―PΨ≠ΙΐBCΒΡ÷–ΒψEΘ§…ηΓ―P«–BD”ΎMΘ°
‘ρCP=2t-4Θ§PM2=PE2=Θ®2t-4Θ©2+22Θ°
Εχ‘ΎRtΓςPMD÷–Θ§”…”ΎΓœPDM=45ΓψΘ§Υυ“‘DP=
PMȧ֥DP2=2PM2Ȱ
ΓύΘ®8-2tΘ©2=2[Θ®2t-4Θ©2+22]Θ°
ΫβΒΟt=Γά
Θ§ΗΚ÷Β…α»ΞΘ§
Γύt=
Θ§
»τΓ―PΨ≠ΙΐCDΒΡ÷–ΒψΘ§Γ―PΒΡΑκΨΕr=2Θ®
-1Θ©Θ§
Ι t=2+
Θ§
Ι Β±ΒψP‘ΎCD…œ‘ΥΕ· ±Θ§»τt=
Μρ2+
Θ§‘ρΓ―P«ΓΚΟΨ≠Ιΐ’ΐΖΫ–ΈABCDΒΡΡ≥“Μ±ΏΒΡ÷–ΒψΘ°
S=S’ΐΖΫ–ΈABCD-SΓςADQ-SΓςBPQ-SΓςPCD=16-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Β±2ΘΦtΓή4 ±Θ§Φ¥ΒψP‘ΎCD…œ ±Θ§DP=8-2tΘ§
S=
| 1 |
| 2 |

Θ®2Θ©ΔΌ»τPD=QDΘ§‘ρRtΓςDCPΓ’RtΓςDAQΘ®HLΘ©Θ°
ΓύCP=AQΘ°Φ¥t=4-2tΘ§ΫβΒΟt=
| 4 |
| 3 |
ΔΎ»τPD=PQΘ§‘ρPD2=PQ2Θ§Φ¥42+Θ®4-2tΘ©2=Θ®4-tΘ©2+Θ®2tΘ©2Θ°
ΫβΒΟt=-4Γά4
| 2 |
| 2 |
| 2 |
Δέ»τQD=PQΘ§‘ρQD2=PQ2Θ§Φ¥16+t2=Θ®4-tΘ©2+Θ®2tΘ©2Θ§ΫβΒΟt=0Μρt=2Θ§
Γύt=
| 4 |
| 3 |
| 2 |
Θ®3Θ©Β±P‘ΎCD…œ‘ΥΕ· ±Θ§»τΓ―PΨ≠ΙΐBCΒΡ÷–ΒψEΘ§…ηΓ―P«–BD”ΎMΘ°
‘ρCP=2t-4Θ§PM2=PE2=Θ®2t-4Θ©2+22Θ°
Εχ‘ΎRtΓςPMD÷–Θ§”…”ΎΓœPDM=45ΓψΘ§Υυ“‘DP=
| 2 |
ΓύΘ®8-2tΘ©2=2[Θ®2t-4Θ©2+22]Θ°
ΫβΒΟt=Γά
| 6 |
Γύt=
| 6 |
»τΓ―PΨ≠ΙΐCDΒΡ÷–ΒψΘ§Γ―PΒΡΑκΨΕr=2Θ®
| 2 |
Ι t=2+
| 2 |
Ι Β±ΒψP‘ΎCD…œ‘ΥΕ· ±Θ§»τt=
| 6 |
| 2 |
ΒψΤάΘΚ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥ’ΐΖΫ–ΈΒΡ–‘÷ Θ§»ΪΒ»»ΐΫ«–ΈΒΡ≈–Ε®Θ§«–œΏΒΡ–‘÷ Β»÷Σ ΕΒψΘ°“ΣΉΔ“βΘ®2Θ©Θ®3Θ©÷–≤ΜΆ§ΒΡ«ιΩω“ΣΫχ––Ζ÷άύΧ÷¬έΘ§≤Μ“ΣΕΣΒτ»ΈΚΈ“Μ÷÷«ιΩωΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 »γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡ±ΏAB”κ’ΐΖΫ–ΈAEFMΒΡ±ΏAM‘ΎΆ§“Μ÷±œΏ…œΘ§÷±œΏBE”κDMΫΜ”ΎΒψNΘ°«σ÷ΛΘΚBNΓΆDMΘ°
»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡ±ΏAB”κ’ΐΖΫ–ΈAEFMΒΡ±ΏAM‘ΎΆ§“Μ÷±œΏ…œΘ§÷±œΏBE”κDMΫΜ”ΎΒψNΘ°«σ÷ΛΘΚBNΓΆDMΘ° Θ®2013•±±μ’«χΡΘΡβΘ©»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΘ§ΒψE «BC…œ“ΜΒψΘ§ΒψF «CD―”≥ΛœΏ…œ“ΜΒψΘ§Ν§Ϋ”EFΘ§»τBE=DFΘ§ΒψP «EFΒΡ÷–ΒψΘ°
Θ®2013•±±μ’«χΡΘΡβΘ©»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΘ§ΒψE «BC…œ“ΜΒψΘ§ΒψF «CD―”≥ΛœΏ…œ“ΜΒψΘ§Ν§Ϋ”EFΘ§»τBE=DFΘ§ΒψP «EFΒΡ÷–ΒψΘ° »γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΘ§ΒψE‘ΎBC±Ώ…œΘ§ΫΪΓςDCE»ΤΡ≥ΒψG–ΐΉΣΒΟΒΫΓςCBFΘ§ΒψF«ΓΚΟ‘ΎAB±Ώ…œΘ°
»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΘ§ΒψE‘ΎBC±Ώ…œΘ§ΫΪΓςDCE»ΤΡ≥ΒψG–ΐΉΣΒΟΒΫΓςCBFΘ§ΒψF«ΓΚΟ‘ΎAB±Ώ…œΘ° »γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏΫΜ”ΎOΘ§ΙΐOΒψΉςOEΓΆOFΘ§Ζ÷±πΫΜABΓΔBC”ΎEΓΔFΘ§»τAE=4Θ§CF=3Θ§‘ρEFΒΡ÷Β «Θ®ΓΓΓΓΘ©
»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏΫΜ”ΎOΘ§ΙΐOΒψΉςOEΓΆOFΘ§Ζ÷±πΫΜABΓΔBC”ΎEΓΔFΘ§»τAE=4Θ§CF=3Θ§‘ρEFΒΡ÷Β «Θ®ΓΓΓΓΘ© »γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏACΘ§BDœύΫΜ”ΎΒψOΘ§E «AC…œΒΡ“ΜΒψΘ§ΙΐΒψAΉςAGΓΆBEΘ§¥ΙΉψΈΣGΘ§AGΫΜBD”ΎΒψFΘ°
»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏACΘ§BDœύΫΜ”ΎΒψOΘ§E «AC…œΒΡ“ΜΒψΘ§ΙΐΒψAΉςAGΓΆBEΘ§¥ΙΉψΈΣGΘ§AGΫΜBD”ΎΒψFΘ°