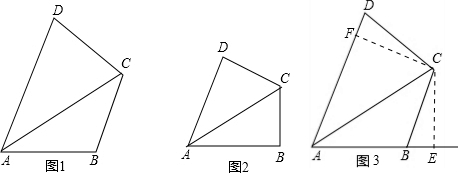
摘要:解决梯形问题.添加辅助线的常见方法: 梯形内平移一腰 梯形外平移一腰 过一腰中点平移另一腰 平移对角线 延长两腰 作高 连结一顶点与腰中点的线段并延长
网址:http://m.1010jiajiao.com/timu3_id_455133[举报]
如图1,在△ABB′和△ACC′中,∠BAB′=∠CAC′=m°,AC=AC′,AB=AB′.
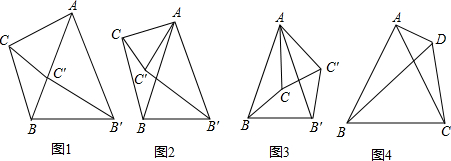
(1)不添加辅助线的前提下,请写出图中满足旋转变换的两个三角形分别是:
(2)线段BC、B′C′的数量关系是:
(3)随着△ACC′绕点A的旋转,(2)的结论是否依然成立?请从图2、图3中任选一个证明你的结论;
(4)利用解决上述问题所获得的经验探索下面的问题:
如图4,等边△ABC外一点D,且∠BDC=60°,连接AD,试探索线段AD、CD、BD的数量关系.
查看习题详情和答案>>

(1)不添加辅助线的前提下,请写出图中满足旋转变换的两个三角形分别是:
△ACB和△AC′B′
△ACB和△AC′B′
;旋转角度是m°
m°
°;(2)线段BC、B′C′的数量关系是:
BC=B′C′
BC=B′C′
;试求出BC、B′C′所在直线的夹角:m°
m°
;(3)随着△ACC′绕点A的旋转,(2)的结论是否依然成立?请从图2、图3中任选一个证明你的结论;
(4)利用解决上述问题所获得的经验探索下面的问题:
如图4,等边△ABC外一点D,且∠BDC=60°,连接AD,试探索线段AD、CD、BD的数量关系.
21、我们在解决数学问题时,经常采用“转化”(或“化归”)的思想方法,把待解决的问题,通过某种转化过程,归结到一类已解决或比较容易解决的问题.
譬如,在学习了一元一次方程的解法以后,进一步研究二元一次方程组的解法时,我们通常采用“消元”的方法,把二元一次方程组转化为一元一次方程;再譬如,在学习了三角形内角和定理以后,进一步研究多边形的内角和问题时,我们通常借助添加辅助线,把多边形转化为三角形,从而解决问题.
问题提出:如何把一个正方形分割成n(n≥9)个小正方形?
为解决上面问题,我们先来研究两种简单的“基本分割法”.
基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.
基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.

问题解决:有了上述两种“基本分割法”后,我们就可以把一个正方形分割成n(n≥9)个小正方形.
(1)把一个正方形分割成9个小正方形.
一种方法:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成4+5=9(个)小正方形.
另一种方法:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成6+3=9(个)小正方形.
(2)把一个正方形分割成10个小正方形.
方法:如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加3×2个小正方形,从而分割成4+3×2=10(个)小正方形.
(3)请你参照上述分割方法,把图⑥给出的正方形分割成11个小正方形(用钢笔或圆珠笔画出草图即可,不用说明分割方法)
(4)把一个正方形分割成n(n≥9)个小正方形.
方法:通过“基本分割法1”、“基本分割法2”或其组合把一个正方形分割成9个、10个和11个小正方形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正方形,从而把一个正方形分割成12个、13个、14个小正方形,依次类推,即可把一个正方形分割成n(n≥9)个小正方形.
从上面的分法可以看出,解决问题的关键就是找到两种基本分割法,然后通过这两种基本分割法或其组合把正方形分割成n(n≥9)个小正方形.
类比应用:仿照上面的方法,我们可以把一个正三角形分割成n(n≥9)个小正三角形.
(1)基本分割法1:把一个正三角形分割成4个小正三角形(请你在图a中画出草图);
(2)基本分割法2:把一个正三角形分割成6个小正三角形(请你在图b中画出草图);
(3)分别把图c、图d和图e中的正三角形分割成9个、10个和11个小正三角形(用钢笔或圆珠笔画出草图即可,不用说明分割方法);

(4)请你写出把一个正三角形分割成n(n≥9)个小正三角形的分割方法(只写出分割方法,不用画图).
查看习题详情和答案>>
譬如,在学习了一元一次方程的解法以后,进一步研究二元一次方程组的解法时,我们通常采用“消元”的方法,把二元一次方程组转化为一元一次方程;再譬如,在学习了三角形内角和定理以后,进一步研究多边形的内角和问题时,我们通常借助添加辅助线,把多边形转化为三角形,从而解决问题.
问题提出:如何把一个正方形分割成n(n≥9)个小正方形?
为解决上面问题,我们先来研究两种简单的“基本分割法”.
基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.
基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.

问题解决:有了上述两种“基本分割法”后,我们就可以把一个正方形分割成n(n≥9)个小正方形.
(1)把一个正方形分割成9个小正方形.
一种方法:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成4+5=9(个)小正方形.
另一种方法:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成6+3=9(个)小正方形.
(2)把一个正方形分割成10个小正方形.
方法:如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加3×2个小正方形,从而分割成4+3×2=10(个)小正方形.
(3)请你参照上述分割方法,把图⑥给出的正方形分割成11个小正方形(用钢笔或圆珠笔画出草图即可,不用说明分割方法)
(4)把一个正方形分割成n(n≥9)个小正方形.
方法:通过“基本分割法1”、“基本分割法2”或其组合把一个正方形分割成9个、10个和11个小正方形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正方形,从而把一个正方形分割成12个、13个、14个小正方形,依次类推,即可把一个正方形分割成n(n≥9)个小正方形.
从上面的分法可以看出,解决问题的关键就是找到两种基本分割法,然后通过这两种基本分割法或其组合把正方形分割成n(n≥9)个小正方形.
类比应用:仿照上面的方法,我们可以把一个正三角形分割成n(n≥9)个小正三角形.
(1)基本分割法1:把一个正三角形分割成4个小正三角形(请你在图a中画出草图);
(2)基本分割法2:把一个正三角形分割成6个小正三角形(请你在图b中画出草图);
(3)分别把图c、图d和图e中的正三角形分割成9个、10个和11个小正三角形(用钢笔或圆珠笔画出草图即可,不用说明分割方法);

(4)请你写出把一个正三角形分割成n(n≥9)个小正三角形的分割方法(只写出分割方法,不用画图).
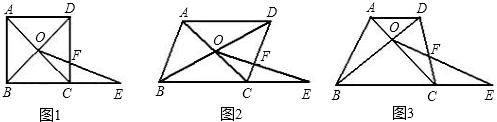
数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线--过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)经过思考,小明认为可以通过添加辅助线--过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
 查看习题详情和答案>>
查看习题详情和答案>>