��Ŀ����
��ѧ���ϣ�����ʦ��ʾ������1����ͼ1���ı���ABCD�������Σ�BC=1���Խ��߽������O����E�DZ�BC�ӳ�����һ�㣮����OE��CD����F����CE=x��CF=y����y����x�ĺ�������ʽ���䶨������1������˼����С����Ϊ����ͨ�����Ӹ�����--����O��OM��BC������ΪM��⣮����Ϊ����뷨��������д������1�Ĵ𰸼���Ӧ���Ƶ����̣�
��2�����������1�е��������ı���ABCD�������Σ�BC=1����Ϊ���ı���ABCD��ƽ���ı��Σ�BC=3��CD=2���������������䣨��ͼ2������ֱ��д�������ı��ĺ�������ʽ��
��3�����������1�е��������ı���ABCD�������Σ�BC=1����һ����Ϊ�����ı���ABCD�����Σ�AD��BC��BC=a��CD=b��AD=c������a��b��cΪ�������������������䣨��ͼ3��������д�������ٴθı��y����x�ĺ�������ʽ�Լ���Ӧ���Ƶ����̣�
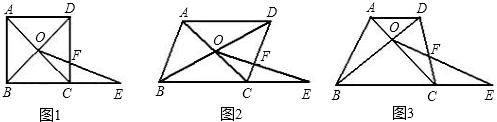
��������1�����ı���ABCD�������Σ��ɵ�OB=OD������OM��BC����֤��OM��DC����ƽ���߷��߶γɱ��������������y����x�ĺ�������ʽ��
��2����OM��CD��BC�ڵ�M�����ã�1���еķ������������y����x�ĺ�������ʽ��
��3��������ON��CD��BC�ڵ�N����ƽ���߷��߶γɱ��������������y����x�ĺ�������ʽ��
��2����OM��CD��BC�ڵ�M�����ã�1���еķ������������y����x�ĺ�������ʽ��
��3��������ON��CD��BC�ڵ�N����ƽ���߷��߶γɱ��������������y����x�ĺ�������ʽ��
���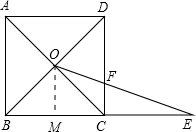 �⣺��1����ͼ��
�⣺��1����ͼ��
���ı���ABCD�������Σ�
��OB=OD��
��OM��BC��
���OMB=��DCB=90�㣬
��OM��DC��
��OM=
DC=
��CM=
BC=
��
��OM��DC��
��
=
��
��
=
��
���y=
��������Ϊx��0��
��2��y=
��x��0����
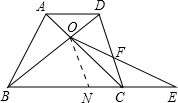
��3������ͼ��
AD��BC��
=
=
��
=
��
����O��ON��CD����BC�ڵ�N��
��
=
��
��ON=
��
��ON��CD��
=
=
��
��
=
��
��CN=
��
��ON��CD��
��
=
����
=
��
��y����x�ĺ�������ʽΪy=
��x��0����
 �⣺��1����ͼ��
�⣺��1����ͼ�����ı���ABCD�������Σ�
��OB=OD��
��OM��BC��
���OMB=��DCB=90�㣬
��OM��DC��
��OM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��OM��DC��
��
| CF |
| OM |
| CE |
| EM |
��
| y | ||
|
| x | ||
x+
|
���y=
| x |
| 2x+1 |
��2��y=
| 2x |
| 2x+3 |

��3������ͼ��
AD��BC��
| BO |
| OD |
| BC |
| AD |
| a |
| c |
| BO |
| BD |
| a |
| a+c |
����O��ON��CD����BC�ڵ�N��
��
| ON |
| DC |
| BO |
| BD |
��ON=
| ab |
| a+c |
��ON��CD��
| CN |
| BN |
| OD |
| BO |
| c |
| a |
��
| CN |
| BC |
| c |
| a+c |
��CN=
| ac |
| a+c |
��ON��CD��
��
| CF |
| ON |
| CE |
| EN |
| y | ||
|
| x | ||
x+
|
��y����x�ĺ�������ʽΪy=
| abx |
| (a+c)x+ac |
���������⿼����ƽ���߷��߶γɱ��������������ͼ�α仯�Ƚ϶࣬�ѶȽϴ���Ĺؼ���ע��ʶͼ��ȷӦ�����ν��˼����⣮

��ϰ��ϵ�д�
�����Ŀ



 ��ѧ���ϣ�����ʦ��ʾ�����⣺��ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB��BF����PΪBC������һ�㣬��AP��PF�����ʣ�AP��PF�������˵�����ɣ�
��ѧ���ϣ�����ʦ��ʾ�����⣺��ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB��BF����PΪBC������һ�㣬��AP��PF�����ʣ�AP��PF�������˵�����ɣ�