摘要:如图8-1.已知P为正方形ABCD的对角线AC上一点(不与A.C重合).PE⊥BC于点E.PF⊥CD于点F. (1) 求证:BP=DP, (2) 如图8-2.若四边形PECF绕点C按逆时针方向旋转.在旋转过程中是否总有BP=DP?若是.请给予证明,若不是.请用反例加以说明, (3) 试选取正方形ABCD的两个顶点.分别与四边形PECF的两个顶点连结.使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等.并证明你的结论 . ⑴ 解法一:在△ABP与△ADP中.利用全等可得BP=DP. 解法二:利用正方形的轴对称性.可得BP=DP. ⑵ 不是总成立 .当四边形PECF绕点C按逆时针方向旋转.点P旋转到BC边上时.DP >DC>BP.此时BP=DP不成立. 说明:未用举反例的方法说理的不得分. ⑶ 连接BE.DF.则BE与DF始终相等. 在图8-1中.可证四边形PECF为正方形. 在△BEC与△DFC中.可证△BEC≌△DFC . 从而有 BE=DF
网址:http://m.1010jiajiao.com/timu3_id_455117[举报]
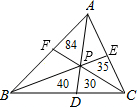 如图所示.已知P为△ABC内一点,AP,BP,CP分别与对边交于D,E,F,把△ABC分成六个小三角形,其中四个小三角形的面积已在图中给出.求△ABC的面积.
如图所示.已知P为△ABC内一点,AP,BP,CP分别与对边交于D,E,F,把△ABC分成六个小三角形,其中四个小三角形的面积已在图中给出.求△ABC的面积. 如图所示,已知∠A为锐角,sinA=
如图所示,已知∠A为锐角,sinA= 47、如图所示,已知E为?ABCD中DC边延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于O,连接OF.
47、如图所示,已知E为?ABCD中DC边延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于O,连接OF.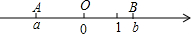 在数轴上表示a,0,1,b四个数的点如图所示,已知O为AB的中点,求a+b+
在数轴上表示a,0,1,b四个数的点如图所示,已知O为AB的中点,求a+b+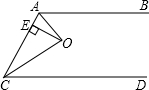 如图所示,已知O为∠A和∠C的平分线的交点,OE⊥AC于E.若OE=2,则O到AB与O到CD的距离之和=
如图所示,已知O为∠A和∠C的平分线的交点,OE⊥AC于E.若OE=2,则O到AB与O到CD的距离之和=