题目内容
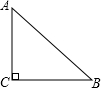如图所示，已知∠A为锐角，sinA=| 8 | 17 |
分析：利用三角函数的定义及勾股定理求解．
解答：解：在Rt△ABC中，∠C=90°，
∵sinA=
=
，
故设BC=8k，AB=17k，由勾股定理，得：
AC=
=
=15k，
∴cosA=
=
=
．tanA=
=
=
．
∵sinA=
| BC |
| AB |
| 8 |
| 17 |
故设BC=8k，AB=17k，由勾股定理，得：
AC=
| AB2-BC2 |
| (17k)2-(8k)2 |
∴cosA=
| AC |
| AB |
| 15k |
| 17k |
| 15 |
| 17 |
| BC |
| AC |
| 8k |
| 15k |
| 8 |
| 15 |
点评：求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
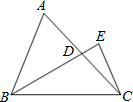如图所示，已知D为边AC的中点，CE垂直于BD的延长线于点E，CE=2cm，S△ABC=8cm2，则线段BD的长为
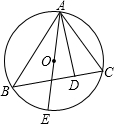如图所示，已知AE为⊙O的直径，AD为△ABC的BC边上的高．
如图所示，已知AB为⊙O的直径，点P为OA上一点，弦MN过点P，且AP=2，OP=3，MP=2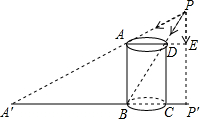
一圆柱形器皿在点光源P下的投影如图所示，已知AD为该器皿底面圆的直径，且AD=3，CD为该器皿的高，CD=4，CP′=1，点D在点P下的投影刚好位于器皿底与器皿壁的交界处，即点B处，点A在点P下的投影为A′，求点A′到CD的距离．
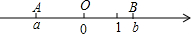在数轴上表示a，0，1，b四个数的点如图所示，已知O为AB的中点，求a+b+