题目内容
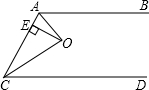如图所示，已知O为∠A和∠C的平分线的交点，OE⊥AC于E．若OE=2，则O到AB与O到CD的距离之和=4
4
．分析：首先过点O作OM⊥AB于点M，作ON⊥CD于点N，由O为∠A和∠C的平分线的交点，OE⊥AC，根据角平分线的性质，可得OM=OE=2，ON=OE=2，继而求得答案．
解答：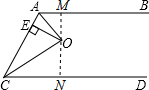
解：过点O作OM⊥AB于点M，作ON⊥CD于点N，
∵O为∠A和∠C的平分线的交点，OE⊥AC，
∴OM=OE=2，ON=OE=2，
∴O到AB与O到CD的距离之和=2+2=4．
故答案为：4．
解：过点O作OM⊥AB于点M，作ON⊥CD于点N，∵O为∠A和∠C的平分线的交点，OE⊥AC，
∴OM=OE=2，ON=OE=2，
∴O到AB与O到CD的距离之和=2+2=4．
故答案为：4．
点评：此题考查了角平分线的性质．此题难度不大，注意辅助线的作法，注意掌握角平分线的定理的应用是关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
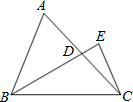如图所示，已知D为边AC的中点，CE垂直于BD的延长线于点E，CE=2cm，S△ABC=8cm2，则线段BD的长为
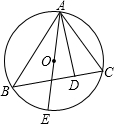如图所示，已知AE为⊙O的直径，AD为△ABC的BC边上的高．
如图所示，已知AB为⊙O的直径，点P为OA上一点，弦MN过点P，且AP=2，OP=3，MP=2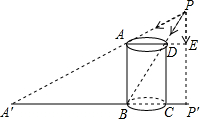
一圆柱形器皿在点光源P下的投影如图所示，已知AD为该器皿底面圆的直径，且AD=3，CD为该器皿的高，CD=4，CP′=1，点D在点P下的投影刚好位于器皿底与器皿壁的交界处，即点B处，点A在点P下的投影为A′，求点A′到CD的距离．
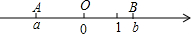在数轴上表示a，0，1，b四个数的点如图所示，已知O为AB的中点，求a+b+