题目内容
 47、如图所示,已知E为?ABCD中DC边延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于O,连接OF.
47、如图所示,已知E为?ABCD中DC边延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于O,连接OF.求证:(1)△ABF≌△ECF;(2)AB=2OF.
分析:(1)由AB∥CD可以得到∠BAF=∠E,∠ABF=∠ECF,再利用DC=CE即可证明△ABF≌△ECF;
(2)根据(1)的结论知道BF=CF,而AO=CO,由此利用中位线定理即可证明题目结论.
(2)根据(1)的结论知道BF=CF,而AO=CO,由此利用中位线定理即可证明题目结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵DC=CE,
∴AB=CE.
∵AB∥CD,
∴∠BAF=∠E,∠ABF=∠ECF.
∴△ABF≌△ECF;
(2)∵△ABF≌△ECF,
∴BF=CF.
又∵四边形ABCD是平行四边形,
∴AO=CO,
∴OF是△ABC的中位线,
∴AB=2OF.
∴AB∥CD,AB=CD.
又∵DC=CE,
∴AB=CE.
∵AB∥CD,
∴∠BAF=∠E,∠ABF=∠ECF.
∴△ABF≌△ECF;
(2)∵△ABF≌△ECF,
∴BF=CF.
又∵四边形ABCD是平行四边形,
∴AO=CO,
∴OF是△ABC的中位线,
∴AB=2OF.
点评:本题考查的是平行四边形的性质及三角形的中位线定理,利用平行四边形的性质,获得全等的条件是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
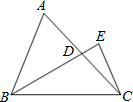 如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为
如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为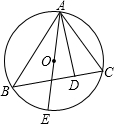 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高. 如图所示,已知AB为⊙O的直径,点P为OA上一点,弦MN过点P,且AP=2,OP=3,MP=2
如图所示,已知AB为⊙O的直径,点P为OA上一点,弦MN过点P,且AP=2,OP=3,MP=2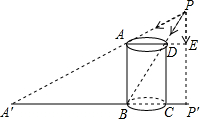 一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.
一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.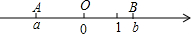 在数轴上表示a,0,1,b四个数的点如图所示,已知O为AB的中点,求a+b+
在数轴上表示a,0,1,b四个数的点如图所示,已知O为AB的中点,求a+b+