摘要:如图.在四边形ABCD中.E.F.G.H分别是AB.BD.CD.AC的中点.要使四边形EFGH是菱形.四边形ABCD还应满足的一个条件是 . 答案:AD=BC.或ABCD为等腰梯形
网址:http://m.1010jiajiao.com/timu3_id_455099[举报]
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?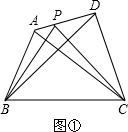
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)当AP=
AD时(如图②):
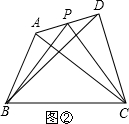
∵AP=
AD,△ABP和△ABD的高相等,
∴S△ABP=
S△ABD.
∵PD=AD-AP=
AD,△CDP和△CDA的高相等,
∴S△CDP=
S△CDA.
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-
S△ABD-
S△CDA
=S四边形ABCD-
(S四边形ABCD-S△DBC)-
(S四边形ABCD-S△ABC)
=
S△DBC+
S△ABC.
(2)当AP=
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(4)一般地,当AP=
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=
AD(0≤
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
查看习题详情和答案>>

探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)当AP=
| 1 |
| 2 |

∵AP=
| 1 |
| 2 |
∴S△ABP=
| 1 |
| 2 |
∵PD=AD-AP=
| 1 |
| 2 |
∴S△CDP=
| 1 |
| 2 |
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-
| 1 |
| 2 |
| 1 |
| 2 |
=S四边形ABCD-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当AP=
| 1 |
| 3 |
(3)当AP=
| 1 |
| 6 |
(4)一般地,当AP=
| 1 |
| n |
问题解决:当AP=
| m |
| n |
| m |
| n |
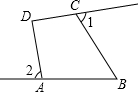 如图,在四边形ABCD中,∠1、∠2分别是∠BCD和∠BAD的邻补角,且∠B+∠ADC=140°,则∠1+∠2等于多少度?
如图,在四边形ABCD中,∠1、∠2分别是∠BCD和∠BAD的邻补角,且∠B+∠ADC=140°,则∠1+∠2等于多少度?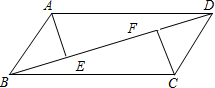 21、如图,在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BF=DE.问四边形ABCD是否为平行四边形?说明你的理由.
21、如图,在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BF=DE.问四边形ABCD是否为平行四边形?说明你的理由.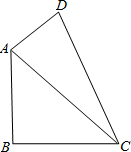 如图,在四边形ABCD中,已知AB=BC=2,CD=3,DA=1,∠B=90°,则∠DAB=
如图,在四边形ABCD中,已知AB=BC=2,CD=3,DA=1,∠B=90°,则∠DAB= 2、如图,在四边形ABCD中,∠A=65°,∠D=105°,∠B的外角是70°,则∠C等于( )
2、如图,在四边形ABCD中,∠A=65°,∠D=105°,∠B的外角是70°,则∠C等于( )