摘要：二次函数的性质 (1)函数y=ax+bx+c(其中a.b.c是常数.且a0)叫做的二次函数. (2)利用配方.可以把二次函数表示成y=a(x+)+或y=a(x-h)+k的形式 (3)二次函数的图象是抛物线.当a＞0时抛物线的开口向上.当a＜0时抛物线开口向下. 抛物线的对称轴是直线x=-或x=h 抛物线的顶点是(-,)或(h,k)
网址：http://m.1010jiajiao.com/timu3_id_454786[举报]
阅读下面的文字后，回答问题：
甲、乙两人同时解答题目：“化简并求值：a+
，其中a=5．”甲、乙两人的解答不同；
甲的解答是：a+
=a+
=a+1-3a=1-2a=-9；
乙的解答是：a+
=a+
=2+3a-1=4a-1=19．
（1） 的解答是错误的．
（2）错误的解答在于未能正确运用二次根式的性质： ．
（3）模仿上题解答：化简并求值：|1-a|+
，其中a=2．
查看习题详情和答案>>
甲、乙两人同时解答题目：“化简并求值：a+
| 1-6a+9a2 |
甲的解答是：a+
| 1-6a+9a2 |
| (1-3a)2 |
乙的解答是：a+
| 1-6a+9a2 |
| (1-3a)2 |
（1）
（2）错误的解答在于未能正确运用二次根式的性质：
（3）模仿上题解答：化简并求值：|1-a|+
| 1-8a+16a2 |
（体验探究题）阅读下面的文字后，回答问题：
题目：已知a+
，其中a=9，先化简式子，再求值．下面为小明和小芳的解答．
小明的解答是：原式=a+
=a+1-a=1．
小芳的解答是：原式=a+
=a+a-1=2a-1=2×9-1=17．
（1） 的解答是错误的．
（2）错误的解答未能正确运用二次根式的性质： = ．
查看习题详情和答案>>
题目：已知a+
| 1-2a+a2 |
小明的解答是：原式=a+
| (1-a)2 |
小芳的解答是：原式=a+
| (1-a)2 |
（1）
（2）错误的解答未能正确运用二次根式的性质：
知识回顾：我们在学习《二次根式》这一章时，对二次根式有意义的条件、性质和运算法则进行了探索，得到了如下结论：
（1）二次根式
有意义的条件是a≥0．
（2）二次根式的性质：①（
）2=a（a≥0）；②
=|a|．
（3）二次根式的运算法则：
①
•
=
（a≥0，b≥0）；
②
=
（a≥0，b＞0）；
③a
±b
=（a±b）
（c≥0）．
类比推广：根据探索二次根式相关知识过程中获得的经验，解决下面的问题．
（1）写出n次根式
（n≥3，n是整数）有意义的条件和性质；
（2）计算
+
．
查看习题详情和答案>>
（1）二次根式
| a |
（2）二次根式的性质：①（
| a |
| a2 |
（3）二次根式的运算法则：
①
| a |
| b |
| ab |
②
| ||
|
|
③a
| c |
| c |
| c |
类比推广：根据探索二次根式相关知识过程中获得的经验，解决下面的问题．
（1）写出n次根式
| n | a |
（2）计算
| 3 | -16 |
| 3 | 2 |
，其中a=5．”甲、乙两人的解答不同；
；
．
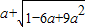，其中a=5．”甲、乙两人的解答不同；
；
．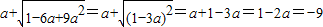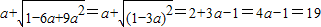