摘要：25．如图.在平面直角坐标系中.把矩形绕点顺时针旋转角.得到矩形．设与交于点.且.且． (1)当时.求直线的解析式, (2)若矩形的对称中心.请探究:当旋转角满足什么条件时.经过点M.且以点为顶点的抛物线经过点D．
网址：http://m.1010jiajiao.com/timu3_id_453932[举报]
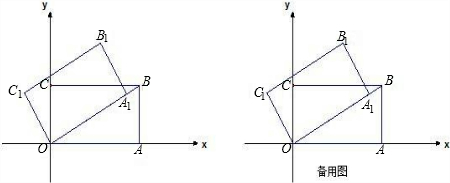
如图，在平面直角坐标系中，A（2
，0），B（2
，2）．把矩形OABC逆时针旋转30°得到矩形OA1B1C1，
（1）求B1点的坐标；
（2）求过点（2，0）且平分矩形OA1B1C1面积的直线l方程；
（3）设（2）中直线l交y轴于点P，直接写出△PC1O与△PB1A1的面积和的值及△POA1与△PB1C1的面积差的值．
查看习题详情和答案>>
| 3 |
| 3 |
（1）求B1点的坐标；
（2）求过点（2，0）且平分矩形OA1B1C1面积的直线l方程；
（3）设（2）中直线l交y轴于点P，直接写出△PC1O与△PB1A1的面积和的值及△POA1与△PB1C1的面积差的值．
查看习题详情和答案>>
如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA=8| 2 |
| 2 |
（1）用t的式子表示△OPQ的面积S；
（2）求证：四边形OPBQ的面积是一个定值，并求出这个定值；
（3）当△OPQ与△PAB和△QPB相似时，抛物线y=
| 1 |
| 4 |
如图，在平面直角坐标系中，矩形OABC的顶点坐标为O（0，0），A（2
，0），B（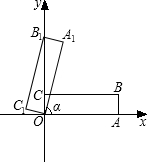
2
，2），把矩形OABC绕点O逆时针方向旋转α度，使点B正好落在y轴正半轴上，得到矩形OA1B1C1．
（1）求角α的度数；
（2）求直线A1B1的函数关系式，并判断直线A1B1是否经过点B，为什么？ 查看习题详情和答案>>
| 3 |
2| 3 |
（1）求角α的度数；
（2）求直线A1B1的函数关系式，并判断直线A1B1是否经过点B，为什么？ 查看习题详情和答案>>
如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长
的速度运动t秒（t＞0），抛物线y=x2+bx+c经过点O和点P，已知矩形ABCD的三个顶点为 A （1，0），B （1，-5），D （4，0）．
（1）求c，b （用含t的代数式表示）：
（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．
①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；
②求△MPN的面积S与t的函数关系式，并求t为何值时，S=
；
（3）在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围． 查看习题详情和答案>>
的速度运动t秒（t＞0），抛物线y=x2+bx+c经过点O和点P，已知矩形ABCD的三个顶点为 A （1，0），B （1，-5），D （4，0）．（1）求c，b （用含t的代数式表示）：
（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．
①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；
②求△MPN的面积S与t的函数关系式，并求t为何值时，S=
| 21 | 8 |
（3）在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围． 查看习题详情和答案>>
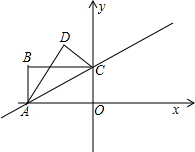如图，在平面直角坐标系中，已知矩形OABC的两个顶点A、B 的坐标分别A（
，0）、B（