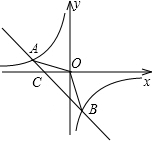（2013•黄石模拟）如图，已知A（-4，n），B（1，-4）是一次函数y=kx+b的图象和反比例函数y=

m

x

的图象的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与x轴的交点C的坐标及△AOB的面积；
（3）求不等式kx+b-

m

x

＜0的解集（请直接写出答案）．

今年春季，由于缺乏市场指导，盲目种植及气候等因素影响，大量应季的南北蔬菜集中上市，致使某些蔬菜的收购价陡跌，北方不少地区的菜农因此陷入困境．以菜农王某所种油菜为例，从今年油菜开始上市，每周收购价y（元/千克）与上市时间x（周）的部分对应值如下表所示．而同时市场售价z（元/千克）与上市时间x（周）的关系如图所示．

x（周）	1	3	4	5
y（元/千克）	3.0	1.05	0.45	0.1

（1）请你从所学的一次函数、二次函数和反比例函数中确定哪种函数能表示y与x以及z与x的变化规律，求出y与x以及z与x的函数关系式；
（2）试问这5周，哪一周油菜的市场售价与收购价的差距最大？求出这个最大差距；
（3）由于供远远大于求以及运输问题，尽管油菜收购价已低至0.1元/千克，不少菜农种植的油菜却仍然无人问津．商务部采取各种措施，发挥地方政府储备和商业储备的应急调节作用，务求帮助菜农解决“卖菜难”问题．从上市第6周开始逐见成效．以菜农王某为例，上市第5周时共售出2吨油菜，有1吨成熟的油菜因为没能售出而烂在地里．从第6周起，销售量比上周增加a%，且收购价也比上周上涨7a%．已知油菜的种植成本为1.2元/千克，假设每周成熟的油菜数量一样．这样一来，第6周的损失比第5周大约少了980元．请你参考以下数据，通过计算估算出a的值．（精确到十分位）
（参考数据：141²=19881，142²=20164，143²=20449，144²=20736，145²=21025）

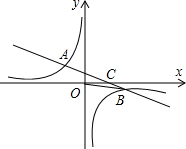（2013•黄石）如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=

k

x

（k≠0）的图象交于二、四象限的A、B两点，与x轴交于C点．已知A（-2，m），B（n，-2），tan∠BOC=

2

5

，则此一次函数的解析式为．

26、3月底，某公司还有11000千克芦柑库存，这些芦柑的销售期最多还有60天，60天后库存的芦柑不能再销售，需要当垃圾处理，处理费为0.05元/千克、经调查得如下数据：

（1）按2元/千克的价格销售，能否在60天内售完这些芦柑？按此价格销售，获得的总毛利润是多少元？（总毛利润=销售总收入-库存处理费）
（2）分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y与x（0＜x≤2）之间的函数关系式；
（3）若要在4月份售完这些芦柑（4月份按30天计算），则销售价格最高可定为多少元/千克？（精确到0.1元/千克）

（2012•黄石）已知抛物线C₁的函数解析式为y=ax²+bx-3a（b＜0），若抛物线C₁经过点（0，-3），方程ax²+bx-3a=0的两根为x₁，x₂，且|x₁-x₂|=4．
（1）求抛物线C₁的顶点坐标．
（2）已知实数x＞0，请证明x+

1

x

≥2，并说明x为何值时才会有x+

1

x

=2．
（3）若将抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线C₂，设A（m，y₁），B（n，y₂）是C₂上的两个不同点，且满足：∠AOB=90°，m＞0，n＜0．请你用含m的表达式表示出△AOB的面积S，并求出S的最小值及S取最小值时一次函数OA的函数解析式．
（参考公式：在平面直角坐标系中，若P（x₁，y₁），Q（x₂，y₂），则P，Q两点间的距离为

(x2-x1)2+(y2-y1)2

）