题目内容
 今年春季,由于缺乏市场指导,盲目种植及气候等因素影响,大量应季的南北蔬菜集中上市,致使某些蔬菜的收购价陡跌,北方不少地区的菜农因此陷入困境.以菜农王某所种油菜为例,从今年油菜开始上市,每周收购价y(元/千克)与上市时间x(周)的部分对应值如下表所示.而同时市场售价z(元/千克)与上市时间x(周)的关系如图所示.
今年春季,由于缺乏市场指导,盲目种植及气候等因素影响,大量应季的南北蔬菜集中上市,致使某些蔬菜的收购价陡跌,北方不少地区的菜农因此陷入困境.以菜农王某所种油菜为例,从今年油菜开始上市,每周收购价y(元/千克)与上市时间x(周)的部分对应值如下表所示.而同时市场售价z(元/千克)与上市时间x(周)的关系如图所示.| x(周) | 1 | 3 | 4 | 5 |
| y(元/千克) | 3.0 | 1.05 | 0.45 | 0.1 |
(2)试问这5周,哪一周油菜的市场售价与收购价的差距最大?求出这个最大差距;
(3)由于供远远大于求以及运输问题,尽管油菜收购价已低至0.1元/千克,不少菜农种植的油菜却仍然无人问津.商务部采取各种措施,发挥地方政府储备和商业储备的应急调节作用,务求帮助菜农解决“卖菜难”问题.从上市第6周开始逐见成效.以菜农王某为例,上市第5周时共售出2吨油菜,有1吨成熟的油菜因为没能售出而烂在地里.从第6周起,销售量比上周增加a%,且收购价也比上周上涨7a%.已知油菜的种植成本为1.2元/千克,假设每周成熟的油菜数量一样.这样一来,第6周的损失比第5周大约少了980元.请你参考以下数据,通过计算估算出a的值.(精确到十分位)
(参考数据:1412=19881,1422=20164,1432=20449,1442=20736,1452=21025)
分析:(1)首先判断出函数关系,再利用待定系数法求出一次函数和二次函数解析式,进而得出答案即可;
(2)根据差距=z-y得出关于x的函数解析式,进而利用公式法求出x=-
时,得出此时差距最大;
(3)根据先求出第5周损失=2000×(1.2-0.1)+1000×1.2=3400,再由题意得出等式方程求出即可.
(2)根据差距=z-y得出关于x的函数解析式,进而利用公式法求出x=-
| b |
| 2a |
(3)根据先求出第5周损失=2000×(1.2-0.1)+1000×1.2=3400,再由题意得出等式方程求出即可.
解答:解:(1)根据图表可得出y与x是二次函数关系,设解析式为:y=ax2+bx+c,
将(1,3.0),(3,1.05),(4,0.45)代入得:
,
解得:
故y与x的函数关系式为:y=
x2-
x+
,
根据图象可以得出z与x是一次函数关系,将(2,6),(5,3)代入z=kx+b得:
,
解得:
故z与x的函数关系式为:z=-x+8;
(2)差距=z-y=-
x2+
x-
.
当x=-
=-
÷[2×(-
)]=
时,有最大差距.
而周数x只能取整数,
故当x=2时,有最大差距为4.1元/千克;
(3)先求出第5周损失=2000×(1.2-0.1)+1000×1.2=3400,再由题意得
2000×(1+a%)[1.2-0.1(1+7a%)]+[3000-2000(1+a%)]×1.2=3400-980
令t=a%,整理得70t2+80t-49=0,
解得:t≈
.
则t1=
≈0.4429,t2=
≈-1.5857(舍).
故a≈44.3.
将(1,3.0),(3,1.05),(4,0.45)代入得:
|
解得:
|
故y与x的函数关系式为:y=
| 1 |
| 8 |
| 59 |
| 40 |
| 87 |
| 20 |
根据图象可以得出z与x是一次函数关系,将(2,6),(5,3)代入z=kx+b得:
|
解得:
|
故z与x的函数关系式为:z=-x+8;
(2)差距=z-y=-
| 1 |
| 8 |
| 19 |
| 40 |
| 87 |
| 20 |
当x=-
| b |
| 2a |
| 19 |
| 40 |
| 1 |
| 8 |
| 19 |
| 10 |
而周数x只能取整数,
故当x=2时,有最大差距为4.1元/千克;
(3)先求出第5周损失=2000×(1.2-0.1)+1000×1.2=3400,再由题意得
2000×(1+a%)[1.2-0.1(1+7a%)]+[3000-2000(1+a%)]×1.2=3400-980
令t=a%,整理得70t2+80t-49=0,
解得:t≈
| -80±142 |
| 140 |
则t1=
| -80+142 |
| 140 |
| -80-142 |
| 140 |
故a≈44.3.
点评:此题主要考查了二次函数的应用和一元二次方程的应用,根据已知得出第5周损失进而表示出关于第6周损失的等式方程是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
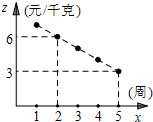 今年春季,由于缺乏市场指导,盲目种植及气候等因素影响,大量应季的南北蔬菜集中上市,致使某些蔬菜的收购价陡跌,北方不少地区的菜农因此陷入困境.以菜农王某所种油菜为例,从今年油菜开始上市,每周收购价y(元/千克)与上市时间x(周)的部分对应值如下表所示.而同时市场售价z(元/千克)与上市时间x(周)的关系如图所示.
今年春季,由于缺乏市场指导,盲目种植及气候等因素影响,大量应季的南北蔬菜集中上市,致使某些蔬菜的收购价陡跌,北方不少地区的菜农因此陷入困境.以菜农王某所种油菜为例,从今年油菜开始上市,每周收购价y(元/千克)与上市时间x(周)的部分对应值如下表所示.而同时市场售价z(元/千克)与上市时间x(周)的关系如图所示.
| x(周) | 1 | 3 | 4 | 5 |
| y(元/千克) | 3.0 | 1.05 | 0.45 | 0.1 |
(2)试问这5周,哪一周油菜的市场售价与收购价的差距最大?求出这个最大差距;
(3)由于供远远大于求以及运输问题,尽管油菜收购价已低至0.1元/千克,不少菜农种植的油菜却仍然无人问津.商务部采取各种措施,发挥地方政府储备和商业储备的应急调节作用,务求帮助菜农解决“卖菜难”问题.从上市第6周开始逐见成效.以菜农王某为例,上市第5周时共售出2吨油菜,有1吨成熟的油菜因为没能售出而烂在地里.从第6周起,销售量比上周增加a%,且收购价也比上周上涨7a%.已知油菜的种植成本为1.2元/千克,假设每周成熟的油菜数量一样.这样一来,第6周的损失比第5周大约少了980元.请你参考以下数据,通过计算估算出a的值.(精确到十分位)
(参考数据:1412=19881,1422=20164,1432=20449,1442=20736,1452=21025)
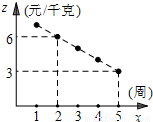 今年春季,由于缺乏市场指导,盲目种植及气候等因素影响,大量应季的南北蔬菜集中上市,致使某些蔬菜的收购价陡跌,北方不少地区的菜农因此陷入困境.以菜农王某所种油菜为例,从今年油菜开始上市,每周收购价y(元/千克)与上市时间x(周)的部分对应值如下表所示.而同时市场售价z(元/千克)与上市时间x(周)的关系如图所示.
今年春季,由于缺乏市场指导,盲目种植及气候等因素影响,大量应季的南北蔬菜集中上市,致使某些蔬菜的收购价陡跌,北方不少地区的菜农因此陷入困境.以菜农王某所种油菜为例,从今年油菜开始上市,每周收购价y(元/千克)与上市时间x(周)的部分对应值如下表所示.而同时市场售价z(元/千克)与上市时间x(周)的关系如图所示.| x(周) | 1 | 3 | 4 | 5 |
| y(元/千克) | 3.0 | 1.05 | 0.45 | 0.1 |
(2)试问这5周,哪一周油菜的市场售价与收购价的差距最大?求出这个最大差距;
(3)由于供远远大于求以及运输问题,尽管油菜收购价已低至0.1元/千克,不少菜农种植的油菜却仍然无人问津.商务部采取各种措施,发挥地方政府储备和商业储备的应急调节作用,务求帮助菜农解决“卖菜难”问题.从上市第6周开始逐见成效.以菜农王某为例,上市第5周时共售出2吨油菜,有1吨成熟的油菜因为没能售出而烂在地里.从第6周起,销售量比上周增加a%,且收购价也比上周上涨7a%.已知油菜的种植成本为1.2元/千克,假设每周成熟的油菜数量一样.这样一来,第6周的损失比第5周大约少了980元.请你参考以下数据,通过计算估算出a的值.(精确到十分位)
(参考数据:1412=19881,1422=20164,1432=20449,1442=20736,1452=21025)