Question

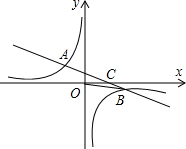（2013•黄石）如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=

k

x

（k≠0）的图象交于二、四象限的A、B两点，与x轴交于C点．已知A（-2，m），B（n，-2），tan∠BOC=

2

5

，则此一次函数的解析式为

y=-x+3

．

Answer 1

分析：过点B作BD⊥x轴，在直角三角形BOD中，根据已知的三角函数值求出OD的长，得到点B的坐标，把点B的坐标代入反比例函数的解析式中，求出反比例函数的解析式，然后把点A的横坐标代入反比例函数的解析式中求出点A的坐标，最后分别把点A和点B的坐标代入一次函数解析式，求出a和b的值即可得到一次函数解析式．

解答：解：过点B作BD⊥x轴，
在Rt△BOD中，∵tan∠BOC=

BD

OD

=

2

OD

=

2

5

，
∴OD=5，
则点B的坐标为（5，-2），
把点B的坐标为（5，-2）代入反比例函数y=

k

x

（k≠0）中，
则-2=

k

5

，即k=-10，
∴反比例函数的解析式为y=-

10

x

，
把A（-2，m）代入y=-

10

x

中，m=5，
∴A的坐标为（-2，5），
把A（-2，5）和B（5，-2）代入一次函数y=ax+b（a≠0）中，
得：

-2a+b=5 5a+b=-2

，解得

a=-1 b=3

，
则一次函数的解析式为y=-x+3．
故答案为：y=-x+3．

点评：此题考查了反比例函数和一次函数的交点问题，以及三角函数值，用待定系数法确定函数的解析式，是常用的一种解题方法．同学们要熟练掌握这种方法．