��Ŀ����
��2012•��ʯ����֪������C1�ĺ�������ʽΪy=ax2+bx-3a��b��0������������C1�����㣨0��-3��������ax2+bx-3a=0������Ϊx1��x2����|x1-x2|=4��
��1����������C1�Ķ������꣮
��2����֪ʵ��x��0����֤��x+
��2����˵��xΪ��ֵʱ�Ż���x+
=2��
��3������������������ƽ��4����λ��������ƽ��1����λ��õ�������C2����A��m��y1����B��n��y2����C2�ϵ�������ͬ�㣬�����㣺��AOB=90�㣬m��0��n��0�������ú�m�ı���ʽ��ʾ����AOB�����S�������S����Сֵ��Sȡ��Сֵʱһ�κ���OA�ĺ�������ʽ��
���ο���ʽ����ƽ��ֱ������ϵ�У���P��x1��y1����Q��x2��y2������P��Q�����ľ���Ϊ
��
��1����������C1�Ķ������꣮
��2����֪ʵ��x��0����֤��x+
| 1 |
| x |
| 1 |
| x |
��3������������������ƽ��4����λ��������ƽ��1����λ��õ�������C2����A��m��y1����B��n��y2����C2�ϵ�������ͬ�㣬�����㣺��AOB=90�㣬m��0��n��0�������ú�m�ı���ʽ��ʾ����AOB�����S�������S����Сֵ��Sȡ��Сֵʱһ�κ���OA�ĺ�������ʽ��
���ο���ʽ����ƽ��ֱ������ϵ�У���P��x1��y1����Q��x2��y2������P��Q�����ľ���Ϊ
| (x2-x1)2+(y2-y1)2 |
��������1���������ߵĶ������꣬��Ҫ����������ߵĽ���ʽ����ȷ������ϵ��a��b��ֵ����֪������ͼ����y�ύ�㣬��ȷ������ʽ�еij�����ɴ˵õ�a��ֵ����Ȼ��ӷ���������b��ֵ����ɸ�����������ľ���ֵ����������ʵ����Σ�ת��Ϊ�����͡�����������ʽ������ϸ���ϵ���Ĺ�ϵ�������b��ֵ��
��2��x•
=1����˽�x+
�����ȫƽ��ʽ��Ȼ�����ƽ���ķǸ��Լ��ɵ�֤��
��3����ϣ�1���������ߵĽ���ʽ�Լ�������ƽ�ƹ��ɣ��ɵó�������C2�Ľ���ʽ����Rt��OAB�У��ɹ��ɶ�����ȷ��m��n�Ĺ�ϵʽ��Ȼ����m�г���AOB���������ʽ����ϲ���ʽ�����֪ʶ��ȷ����OAB����С���ֵ�Լ���ʱm��ֵ�������ɴ���ϵ����ȷ��һ�κ���OA�Ľ���ʽ��
��2��x•
| 1 |
| x |
| 1 |
| x |
��3����ϣ�1���������ߵĽ���ʽ�Լ�������ƽ�ƹ��ɣ��ɵó�������C2�Ľ���ʽ����Rt��OAB�У��ɹ��ɶ�����ȷ��m��n�Ĺ�ϵʽ��Ȼ����m�г���AOB���������ʽ����ϲ���ʽ�����֪ʶ��ȷ����OAB����С���ֵ�Լ���ʱm��ֵ�������ɴ���ϵ����ȷ��һ�κ���OA�Ľ���ʽ��
����⣺��1���������߹���0��-3���㣬��-3a=-3
��a=1
��y=x2+bx-3
��x2+bx-3=0������Ϊx1��x2��|x1-x2|=4
��|x1-x2|=
=4����b��0
��b=-2
��y=x2-2x-3=��x-1��2-4
��������C1�Ķ�������Ϊ��1��-4����
��2����x��0����x+
-2=��
-
��2��0
��x+
��2����Ȼ��x=1ʱ������x+
=2��
��3����ƽ��֪ʶ��C2�Ľ���ʽΪ��y=x2
��A��m��m2����B��n��n2��
�ߡ�AOBΪֱ�������Σ�
��OA2+OB2=AB2
��m2+m4+n2+n4=��m-n��2+��m2-n2��2
����ã�mn=-1
��S��AOB=
=
=
=
=
=
��m+
����
•2=1
��S��AOB����СֵΪ1����ʱm=1��A��1��1��
��ֱ��OA��һ�κ�������ʽΪy=x��
��a=1
��y=x2+bx-3
��x2+bx-3=0������Ϊx1��x2��|x1-x2|=4
��|x1-x2|=
| (x1+x2)2-4x1x2 |
��b=-2
��y=x2-2x-3=��x-1��2-4
��������C1�Ķ�������Ϊ��1��-4����
��2����x��0����x+
| 1 |
| x |
| x |
| 1 | ||
|
��x+
| 1 |
| x |
| 1 |
| x |
��3����ƽ��֪ʶ��C2�Ľ���ʽΪ��y=x2
��A��m��m2����B��n��n2��
�ߡ�AOBΪֱ�������Σ�
��OA2+OB2=AB2
��m2+m4+n2+n4=��m-n��2+��m2-n2��2
����ã�mn=-1
��S��AOB=
| 1 |
| 2 |
| (m+n)2 |
| 1 |
| 2 |
| m2+n2+2mn |
| 1 |
| 2 |
| 2+m2+n2 |
| 1 |
| 2 |
2+m2+
|
=
| 1 |
| 2 |
(m+
|
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| 2 |
��S��AOB����СֵΪ1����ʱm=1��A��1��1��
��ֱ��OA��һ�κ�������ʽΪy=x��
���������⿼���˶��κ�������ʽ��ȷ��������ͼ���ƽ�ơ�����ʽ��Ӧ�õ�֪ʶ�������������ȫƽ��ʽ�ı��α�����ἰ��Ӧ�������ղ������Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
 ��2012•��ʯ����ͼ��ʾ����֪A��ӣ�1��0�����������ÿ��1����λ�����ٶ�����x����������˶�������t�����O��AΪ����������OABC��ʹB��C�㶼�ڵ�һ�����ڣ��ҡ�AOC=60�㣬����P��0��4��ΪԲ�ģ�PCΪ�뾶��Բǡ����OA���ڵ�ֱ�����У���t=
��2012•��ʯ����ͼ��ʾ����֪A��ӣ�1��0�����������ÿ��1����λ�����ٶ�����x����������˶�������t�����O��AΪ����������OABC��ʹB��C�㶼�ڵ�һ�����ڣ��ҡ�AOC=60�㣬����P��0��4��ΪԲ�ģ�PCΪ�뾶��Բǡ����OA���ڵ�ֱ�����У���t=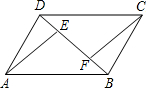 ��2012•��ʯ����ͼ��ʾ����֪��ƽ���ı���ABCD�У�BE=DF����֤����DAE=��BCF��
��2012•��ʯ����ͼ��ʾ����֪��ƽ���ı���ABCD�У�BE=DF����֤����DAE=��BCF��