摘要:16.如图.已知.以点A为圆心.以AO长为半径的圆交轴于另一点B.过点B作BF∥AE交⊙A于点F.直线FE交x轴于点C. (1)求证:直线FC是⊙a的切线, (2)求点C的坐标及直线FC的解析式, (3)有一个半径与⊙A的半径相等.且圆心在轴上运动的⊙P.若⊙P与直线FC相交于M.N两点.是否存在这样的点P.使△PMN是直角三角形.若存在.求出点P的坐标,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_451014[举报]
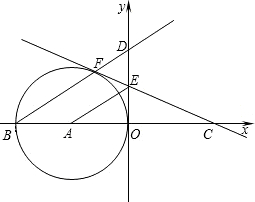
如图,在平面直角坐标系中,以点A(-1,0)为圆心,AO为半径的圆交x 轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF=2
轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF=2
.
(1)求点C的坐标;
(2)求证:AE∥BF;
(3)延长BF交y轴于点D,求点D的坐标及直线BD的解析式. 查看习题详情和答案>>
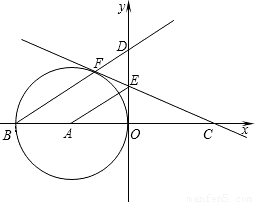
 轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF=2
轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF=2| 2 |
(1)求点C的坐标;
(2)求证:AE∥BF;
(3)延长BF交y轴于点D,求点D的坐标及直线BD的解析式. 查看习题详情和答案>>
 轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF=
轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF= .
. .
.
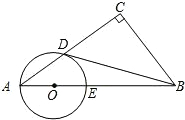 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.