摘要:(一)判断题: 1.已知.( ) 2.已知.( ) 3.若的比例中项. ( ) 4.如图:DE∥BC,EF∥AB,则( ) A D E B F C 5.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,则.( ) 6.有一组邻边对应成比例的两个矩形相似. ( ) 7.如图已知DE∥BC,CD,EB交于O, A S△POE:S△COB=4:9,则.( ) D E B C 8.已知△ABC中,∠BAC=Rt∠,AD⊥BC,AB=2AC,则AD:BC=2:5. ( ) 9.所有的等腰直角三角形都相似. ( ) 10.两个相似多边形的面积比为5,周长比是m,则.( )
网址:http://m.1010jiajiao.com/timu3_id_450433[举报]
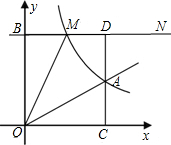 附加题:已知:如图,正比例函数y=ax的图象与反比例函数y=
附加题:已知:如图,正比例函数y=ax的图象与反比例函数y=| k | x |
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值;
(3)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MN∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由. 查看习题详情和答案>>
阅读下面解题过程,判断是否正确.若正确,则在题后的横线上写“正确”两字;若错误,则在题后的横线上写上开始出现错误的那一步的序号,并写出正确的解题过程.
题:已知a=20,b=15,求
-
的值.
解:原式=
-
…①
=样
-
…②
=(a-
b)
-(
a-b)
…③
=(a-
b-
a+b)
…④
=
(a+b)
…⑤
当a=20,b=15时,原式=35
…⑥
答案:③ 查看习题详情和答案>>
题:已知a=20,b=15,求
a3-a2b+
|
|
解:原式=
a(a2-ab+
|
a(
|
=样
a(a-
|
a(
|
=(a-
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| a |
=(a-
| 1 |
| 2 |
| 1 |
| 2 |
| a |
=
| 1 |
| 2 |
| a |
当a=20,b=15时,原式=35
| 5 |
答案:③ 查看习题详情和答案>>
 (附加题)已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(附加题)已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)求△ABC的面积;
(4)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(5)在(4)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
课堂上,李老师出了这样一道题:
已知x=2008-5
,求代数式
÷(1+
)的值.
小明觉得没有好方法,只能直接代入计算,小敏认为只要先化简,就能轻松解答,请你来判断,谁的说法更有道理、并写出你的解答过程.
查看习题详情和答案>>
已知x=2008-5
| 3 |
| x2-2x+1 |
| x2-1 |
| x-3 |
| x+1 |
小明觉得没有好方法,只能直接代入计算,小敏认为只要先化简,就能轻松解答,请你来判断,谁的说法更有道理、并写出你的解答过程.
(附加题)已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)求△ABC的面积;
(4)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(5)在(4)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)求△ABC的面积;
(4)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(5)在(4)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>