��Ŀ����
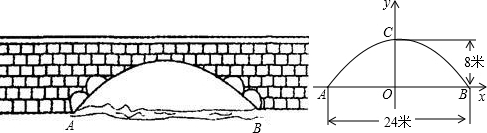
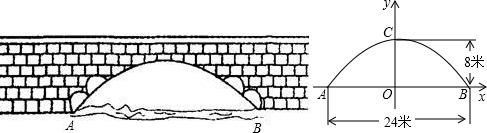
 �������⣩��֪��������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB��OC���Ƿ���x2-10x+16=0�����������������ߵĶԳ�����ֱ��x=-2��
�������⣩��֪��������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB��OC���Ƿ���x2-10x+16=0�����������������ߵĶԳ�����ֱ��x=-2����1����A��B��C��������ꣻ
��2����������ߵı���ʽ��
��3�����ABC�������
��4������E���߶�AB�ϵ�һ�����㣨���A����B���غϣ�������E��EF��AC��BC�ڵ�F������CE����AE�ij�Ϊm����CEF�����ΪS����S��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��5���ڣ�4���Ļ�������˵��S�Ƿ�������ֵ�������ڣ������S�����ֵ���������ʱ��E�����꣬�жϴ�ʱ��BCE����״���������ڣ���˵�����ɣ�
��������1���Ƚ�һԪ���η��̣��õ��߶�OB��OC�ij���Ҳ�͵õ��˵�B��C�������꣬���������ߵĶԳ��Կɵõ�A���ꣻ
��2����A��B��C���������κ�������ʽ������ö��κ�������ʽ��
��3������A��B��C��������ó�AB��CO�ij������ɵó���ABC�������
��4����S��EFC=S��BCE-S��BFE��ֻ������ƽ�еõ����������ƣ����EF��������������Ƚǵ�����ֵ��á�BEF��BE���ϵĸߣ�
��5�����ö��κ��������ֵ��������õ�E���꣮OC��ֱƽ��BE����ôEC=BC��������������ǵ��������Σ�
��2����A��B��C���������κ�������ʽ������ö��κ�������ʽ��
��3������A��B��C��������ó�AB��CO�ij������ɵó���ABC�������
��4����S��EFC=S��BCE-S��BFE��ֻ������ƽ�еõ����������ƣ����EF��������������Ƚǵ�����ֵ��á�BEF��BE���ϵĸߣ�
��5�����ö��κ��������ֵ��������õ�E���꣮OC��ֱƽ��BE����ôEC=BC��������������ǵ��������Σ�
����⣺��1���ⷽ��x2-10x+16=0��x1=2��x2=8��
�ߵ�B��x����������ϣ���C��y����������ϣ���OB��OC��
���B��������2��0������C��������0��8����
�֡�������y=ax2+bx+c�ĶԳ�����ֱ��x=-2��
���������ߵĶԳ��Կɵõ�A������Ϊ��-6��0����
��2���ߵ�C��0��8����������y=ax2+bx+c��ͼ���ϣ�
��c=8����A��-6��0����B��2��0���������ʽ��
�ã�
��
���
��
�����������ߵı���ʽΪy=-
x2-
x+8��
��3���ߵ�B������Ϊ��2��0������C������Ϊ��0��8������A������Ϊ��-6��0����
��AB=2+6=8��CO=8��
���ABC�������S��ABC=
��AB��CO=
��8��8=32��
��4�������⣬AE=m����BE=8-m��
��OA=6��OC=8��
��AC=10
��EF��AC
���BEF�ס�BAC
��
=
����
=
��EF=
��6�֣�
����F��FG��AB������ΪG��
��sin��FEG=sin��CAB=
��
��
=
��
��FG=
•
=8-m��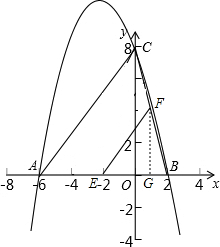
��S=S��BCE-S��BFE=
��8-m����8-
��8-m����8-m����
=
��8-m����8-8+m��=
��8-m��m=-
m2+4m��
�Ա���m��ȡֵ��Χ��0��m��8��
��5�����ڣ�
���ɣ���S=-
m2+4m=-
��m-4��2+8��-
��0��
�൱m=4ʱ��S�����ֵ��S���ֵ=8��
��m=4��
���E��������-2��0����
���BCE����������
�ߵ�B��x����������ϣ���C��y����������ϣ���OB��OC��
���B��������2��0������C��������0��8����
�֡�������y=ax2+bx+c�ĶԳ�����ֱ��x=-2��
���������ߵĶԳ��Կɵõ�A������Ϊ��-6��0����
��2���ߵ�C��0��8����������y=ax2+bx+c��ͼ���ϣ�
��c=8����A��-6��0����B��2��0���������ʽ��
�ã�
|
���
|
�����������ߵı���ʽΪy=-
| 2 |
| 3 |
| 8 |
| 3 |
��3���ߵ�B������Ϊ��2��0������C������Ϊ��0��8������A������Ϊ��-6��0����
��AB=2+6=8��CO=8��
���ABC�������S��ABC=
| 1 |
| 2 |
| 1 |
| 2 |
��4�������⣬AE=m����BE=8-m��
��OA=6��OC=8��
��AC=10
��EF��AC
���BEF�ס�BAC
��
| EF |
| AC |
| BE |
| AB |
| EF |
| 10 |
| 8-m |
| 8 |
��EF=
| 40-5m |
| 4 |
����F��FG��AB������ΪG��
��sin��FEG=sin��CAB=
| 4 |
| 5 |
��
| FG |
| EF |
| 4 |
| 5 |
��FG=
| 4 |
| 5 |
| 40-5m |
| 4 |

��S=S��BCE-S��BFE=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�Ա���m��ȡֵ��Χ��0��m��8��
��5�����ڣ�
���ɣ���S=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�൱m=4ʱ��S�����ֵ��S���ֵ=8��
��m=4��
���E��������-2��0����
���BCE����������
������������Ҫ������һԪ���η��̵Ľⷨ���ô���ϵ��������κ�������ʽ�Լ�����κ�������ֵ��֪ʶ�㣬�ؼ��Ǹ�������ȷ�����κ���ʽ�����s��m�ĺ�����ϵʽ���Լ������Ƿ������ֵ��ȷ�������ε���״��

��ϰ��ϵ�д�
 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
 m���㴬����̽���˴��ܷ����£�˵�����ɣ�
m���㴬����̽���˴��ܷ����£�˵�����ɣ�